Пропорциональные отрезки. Теорема Фалеса

Отношением отрезков длиной a и b называется частное их длин, т. е. $\frac{a}{b}$ .

Отношение показывает, сколько раз отрезок b укладывается в отрезок а. Или, отношение показывает, во сколько раз отрезок а больше отрезка b.

Теорема Фалеса: параллельные прямые, пересекающие стороны угла, отсекают на сторонах этого угла пропорциональные отрезки.

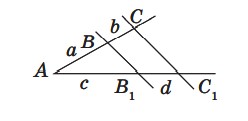
Биссектриса делит противолежащую сторону на отрезки пропорциональные прилежащим сторонам.

Задачи для тренировки

1. Определите, являются ли отрезки длиной a и b пропорциональными отрезкам c и d, если: а) a = 8 см, b = 24 см, c = 4 см, d = 12 см; б) a = 9 см, b = 14 см, c = 7 см, d = 18 см.

2. Прямая MN параллельна основаниям трапеции ABCD. Найдите: а) сторону CD, если AM:AB= 4:5, CN = 3 см; б) сторону AB, если AM:ND= 3:2,
CN = 2 см, AM = 9 см.
3. Прямая MN параллельна основаниям трапеции ABCD. Найдите сторону AB, если AM-MB= 1 см, CN:CD= 3:7.

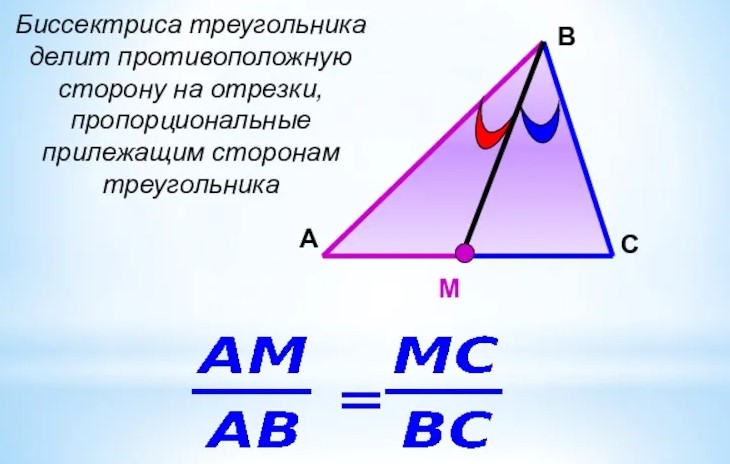
4. По данным рисунка найдите x, если a||b.

5. Найдите отношение отрезков AB и СD, если их длины равны соответственно 15 см и 20 см. Изменится ли это отношение, если длины отрезков перевести в миллиметры?

6. Докажите, что биссектриса делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.

7. Отрезок BD является биссектрисой треугольника АВС. Найдите АВ, если ВС=9 см, AD=7,5 см, DС=4,5 см; б) Найдите DC, если АВ=30, AD=20, BC=16.

8. Отрезок AD является биссектрисой треугольника АВС. Найдите BD и DC, если АВ=14 см, ВС=20 см, АС=21 см.

9. Биссектриса AD треугольника АВС делит сторону ВС на отрезки CD и BD, равные соответственно 4,5 см и 13,5 см. Найдите АВ и АС, если периметр треугольника АВС равен 42 см.

10. В треугольник МNK вписан ромб MDEF так, что вершины D,E,F лежат на сторонах MN, NK, MK. Найдите отрезки NE и EK, если MN=7 см, NK=6 см, МК=5см.

11. Периметр треугольника CDE равен 55 см. В этот треугольник вписан ромб DMFN так, что вершины М, F, N лежат соответственно на сторонах CD, CE, DE. Найдите стороны CD и DE, если CF =8 см, EF=12 см.

12. Найдите отношение отрезков AB и СD, если их длины равны соответственно 18 см и 24 см. Изменится ли это отношение, если длины отрезков перевести в дециметры?

13. Найдите х из пропорции:

а) $\frac{x}{75}=\frac{7}{3}$ ; б) $\frac{21}{x}=\frac{3}{2}$ ; в)2 $\frac{1}{2}$ :0,6x=1,1:0,5; г) 4 $\frac{1}{3}$ :0,2x=1,3:0,3.

14. Точка М делит отрезок АВ на два таких отрезка, что АМ:МВ=1:2. Найдите АМ:АВ и МВ:АВ.

15. Точки С и D делят отрезок АВ на три таких отрезка, что АС:СD:DB=2:3:1. Найдите: а) AD:DB; б) CD:DB; в) СВ:АС; г) АВ:СD.

16.

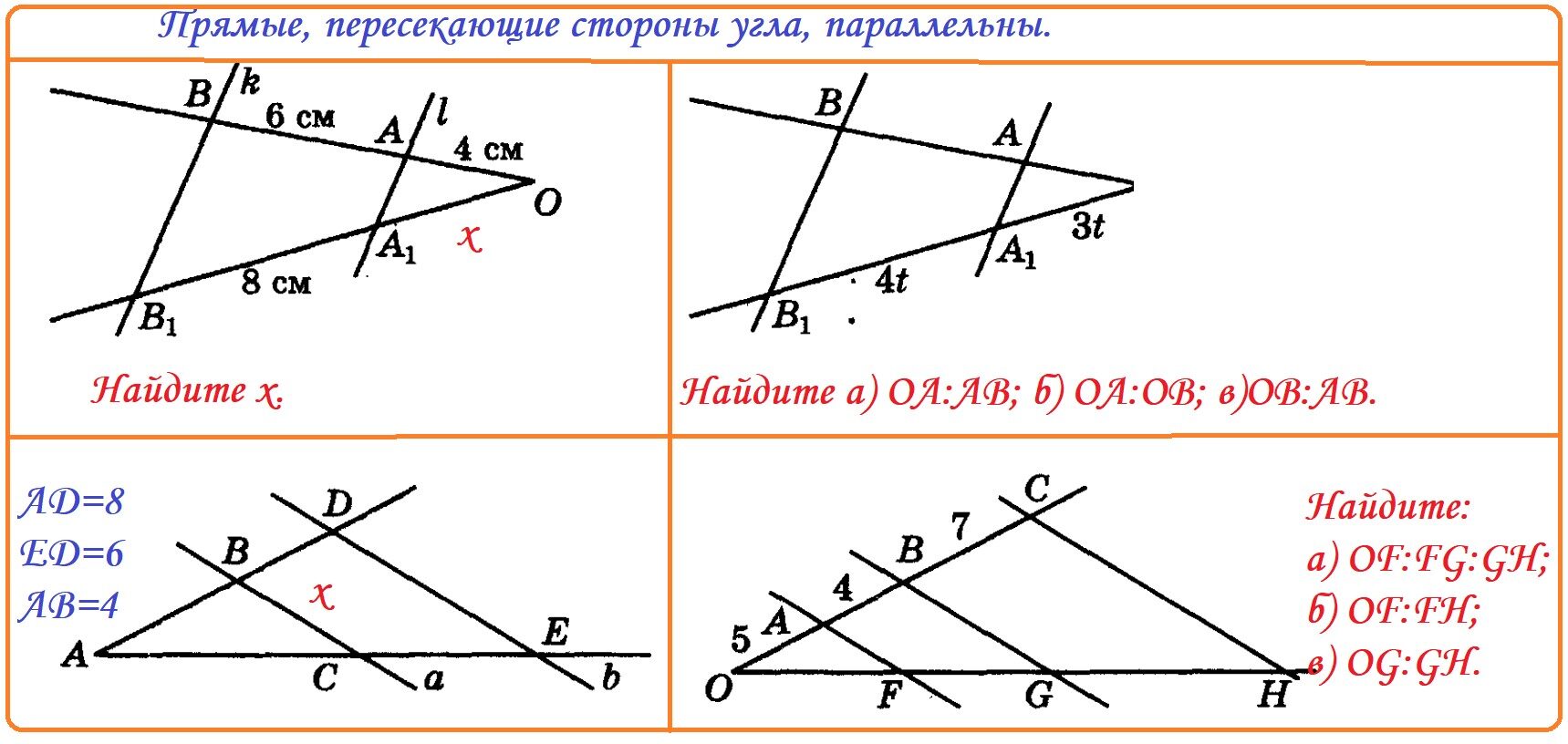
17.

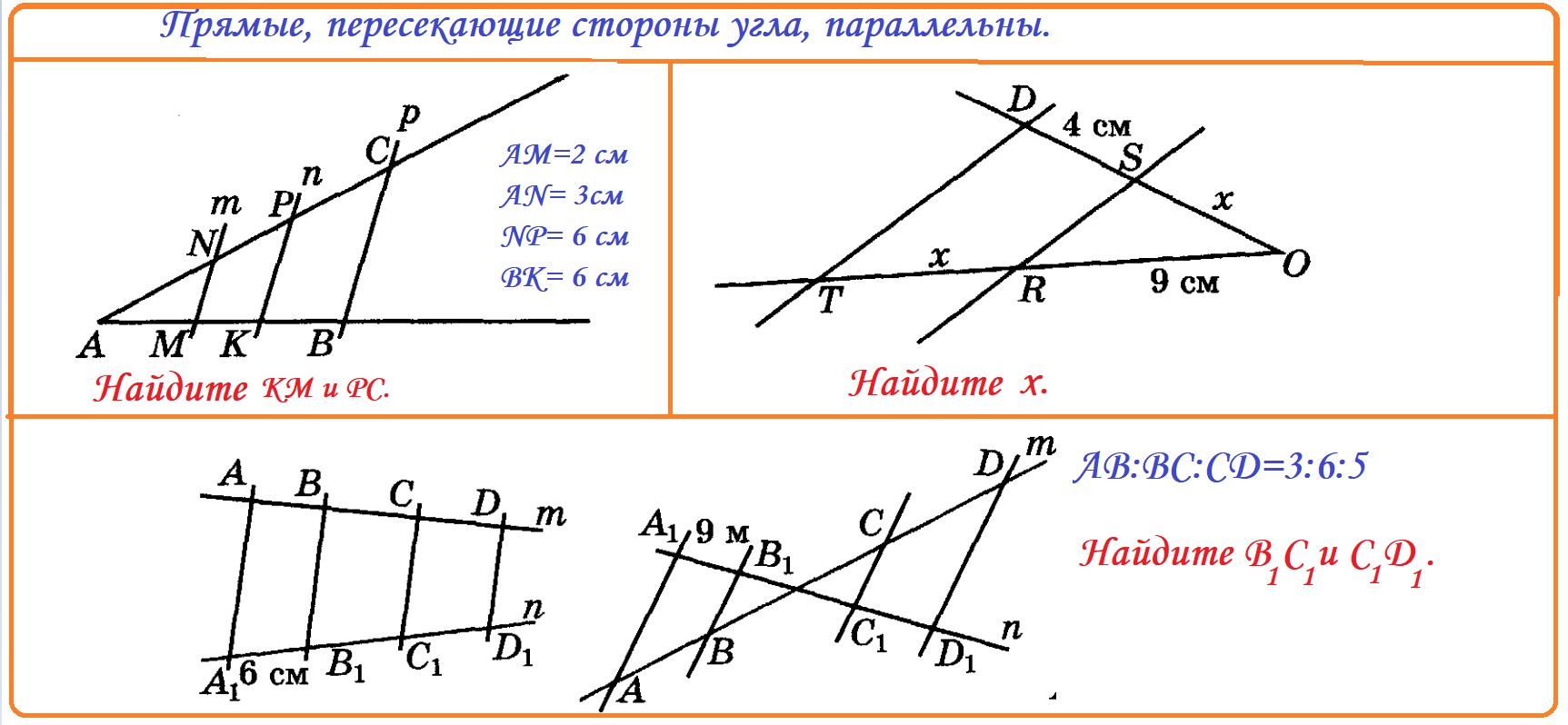
18. На сторонах АВ и АС треугольника АВС отметили соответственно точки М и Р так, что АМ:АВ=3:4, АР:АС=3:4. Найдите длину отрезка МР, если ВС=10 см.

19. На сторонах АВ и АС треугольника АВС отметили соответственно точки М и Р так, что ВМ:ВА=ВР:ВС=1:3. Точки D и Е делят сторону АС на три равные части (АD=DE=ЕС). Докажите, что МD=РЕ.

20. Точка М делит медиану АК треугольника АВС так, что МК=2АМ. В каком отношении прямая ВМ делит сторону АС этого треугольника?

21. Прямая ВК делит сторону АС треугольника АВС в отношении 1:3, считая от вершины С. В каком отношении она делит медиану АМ?

22. Медиана ВМ делит высоту АН треугольника АВС в отношении 3:1, считая от вершины. В каком отношении делит высота эту медиану?

23. .

[свернуть]