1. Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны (определение).
2. Параллелограмм является выпуклым четырехугольником.
3. В параллелограмме противоположные стороны и углы равны (свойство параллелограмма).
4. Диагонали параллелограмма точкой пересечения делятся пополам (свойство параллелограмма).
5. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм (признак параллелограмма).
6. Если в четырехугольнике противолежащие стороны попарно равны, то этот четырехугольник — параллелограмм (признак параллелограмма).
7. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм (признак параллелограмма).
8. Прямоугольник, ромб, квадрат являются параллелограммами.
9. Параллелограмм, у которого все углы равны, называется прямоугольником (определение).
10. Диагонали прямоугольника равны (свойство прямоугольника).
11. Если в параллелограмме диагонали равны, то этот параллелограмм прямоугольник (признак прямоугольника).
12. Параллелограмм, у которого все стороны равны, называется ромбом (определение).
13. Диагонали ромба взаимно перпендикулярны и делят его углы пополам (свойство ромба).
14. Параллелограмм, у которого все стороны и углы равны, называется квадратом (определение).
15. Квадратом называется прямоугольник, у которого все стороны равны.
16. Каждый квадрат является ромбом, но не каждый ромб является квадратом. Ромб является квадратом, если все его углы равны (90º).
17. Каждый квадрат является прямоугольником, но не каждый прямоугольник является квадратом.
18. Все углы квадрата и прямоугольника прямые.
19. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
20. Равные параллелограммы имеют равные площади.
21. Если параллелограмм разбит на несколько многоугольников, то площадь параллелограмма равна сумме площадей этих многоугольников.
22. Если площади параллелограммов равны, то параллелограммы называются равновеликими.
22. Высоту параллелограмма проводят от одной параллельной стороны к другой.
23. Высота параллелограмма может выходить за пределы фигуры, если она проведены из острого угла. В этом случае она опускается на продолжение противолежащей стороны. Все высоты равны только у ромбов и квадратов. В общем случае у любого параллелограмма 2 разных по значению высоты.
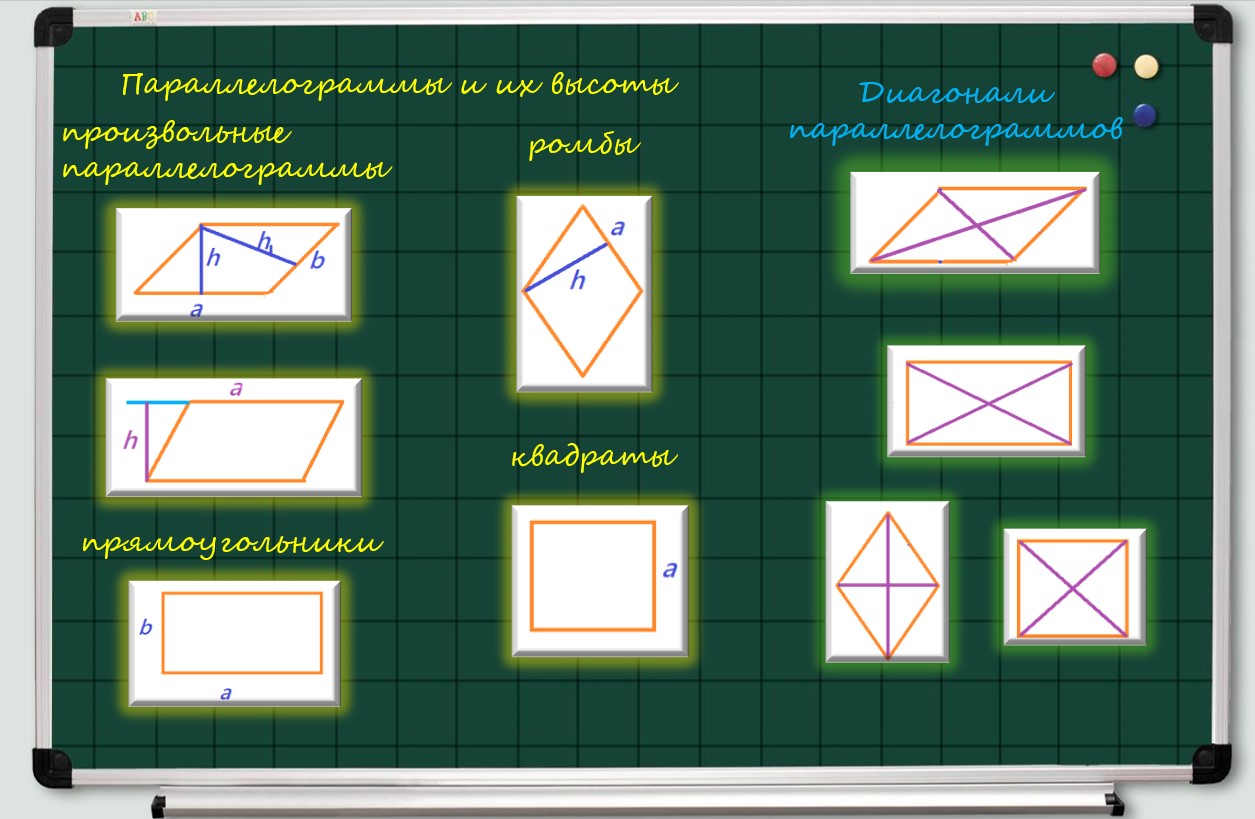
24. Площадь параллелограмма:
- S=a•h, h — высота параллелограмма, а — сторона параллелограмма, к которой проведена высота (формула справедлива для всех параллелограммов);
- S=a•b•sinα, a — сторона параллелограмма, b — сторона параллелограмма, α — угол между сторонами параллелограмма (формула справедлива для всех параллелограммов);
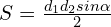 , d1, d2 — диагонали параллелограмма, α — угол между диагоналями параллелограмма (формула справедлива для всех параллелограммов);
, d1, d2 — диагонали параллелограмма, α — угол между диагоналями параллелограмма (формула справедлива для всех параллелограммов);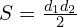 , d1, d2 — диагонали параллелограмма (формула справедлива только для ромбов и квадратов);
, d1, d2 — диагонали параллелограмма (формула справедлива только для ромбов и квадратов);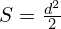 , d — диагональ квадрата (формула справедлива только для квадратов);
, d — диагональ квадрата (формула справедлива только для квадратов);- S=ab, a — сторона прямоугольника, b — сторона прямоугольника (формула справедлива только для прямоугольников);
- S=a², а — сторона квадрата (формула справедлива только для квадрата);
25. Периметр любого параллелограмма — это сумма длин всех (четырех) сторон:
- Р=а+а+b+b=2a+2b=2(a+b), a- сторона параллелограмма, b — сторона параллелограмма (формула справедлива для всех параллелограммов);
- Р=а+а+а+а=4а, а — сторона параллелограмма (формула справедлива для ромбов и квадратов);
26. Не любой параллелограмм можно вписать в окружность. Любой прямоугольник и квадрат можно вписать в окружность.
27. Не в любой параллелограмм можно вписать окружность. В любой квадрат и ромб можно вписать окружность.