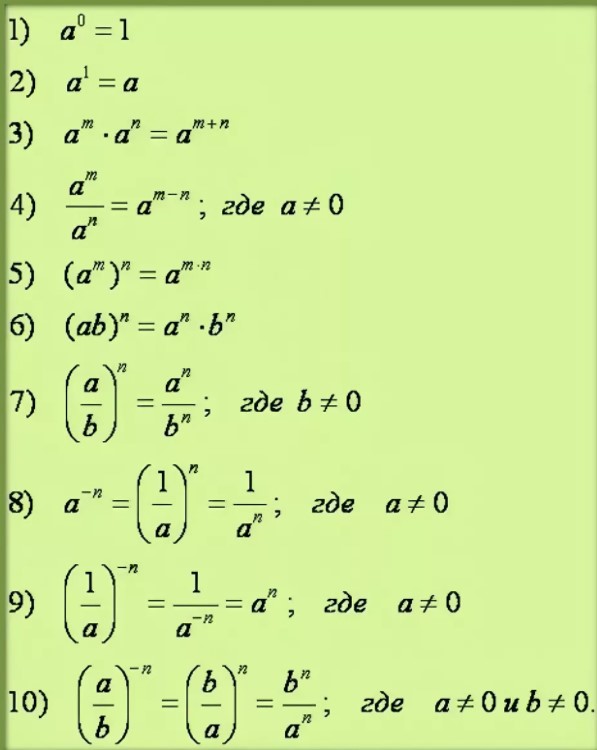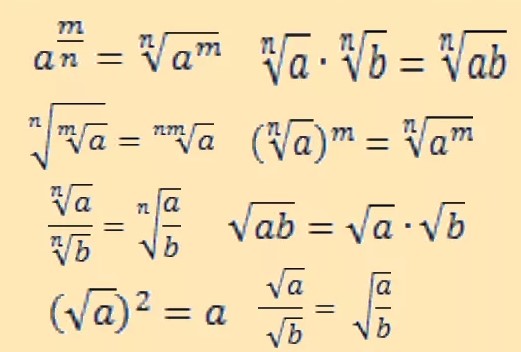Задание № 7
Использование формул для решения задач
- базовый уровень сложности;
- рекомендуемое время выполнения — 5 минут;
- за верное решение можно получить 1 балл;
- решение не проверяется, на апелляцию не подается;
- все необходимые знания и умения формируются в 6-11 классах;
Основные типы заданий
- Формулы с корнями.
- Формулы с тригонометрией.
- Формулы со степенями.
- Формулы с дробями.
- Формулы с логарифмами.
- Квадратные уравнения.
- Задачи с двумя формулами.
- Линейные уравнения.
- Формулы с показательными выражениями.
Алгоритм
- Главное правило: все данные нужно просто подставить в формулу (ее дают) и решить получившееся уравнение.
- Помним о переводе единиц измерения.
- Подставлять единицы измерения в формулу не надо.
Общие правила
- Если уравнение обычное (линейное, у переменной степень 1), то решаем его как во втором классе: все что с буквой на одну сторону, свободные числа на другую.
- Если нужно найти множитель, то произведение делим на второй множитель.
- Если нужно найти слагаемое, то из суммы вычитаем второе слагаемое.
- Если нужно найти делимое, то частное умножаем на делитель.
- Если нужно найти делитель, то делимое делим на частное.
- Если нужно найти уменьшаемое, то к разности прибавляем вычитаемое.
- Если нужно найти вычитаемое, нужно из уменьшаемого вычесть разность.
Формулы сокращенного умножения: 9. Если слева и справа от знака равно по одной дроби, то перемножаем крест-накрест.
9. Если слева и справа от знака равно по одной дроби, то перемножаем крест-накрест.
10. Если с одной стороны дробь, а с другой целое число или целое выражение, то дописываем к целому знаменатель 1 и перемножаем крест-накрест.
11. Если в уравнении есть смешанные числа, то удобнее будет работать, если Вы переведете их в неправильные дроби.
12. Если уравнение полное квадратное (у буквы вторая степень), все переносим в одну сторону, ищем дискриминант и корни или используем теорему Виета.
13. Если неполное квадратное уравнение, то переносим все в одну сторону, вынести общий множитель за скобку, далее каждый множитель приравниваем к нулю по отдельности и решаем обычные линейные уравнения. Или переносим все в одну сторону и раскладываем уравнение по формуле сокращенного умножения (разность квадратов).
14. Если кроме логарифмов есть свободные числа, то превращаем их в логарифмы с таким же основанием, далее объединяем получившиеся логарифмы. Основание логарифма пишется внизу. Подлогарифмическое выражение пишется рядом с буквами log.
15. При работе с логарифмическими выражениями лучше избегать десятичных дробей.
16. Если в уравнении с обеих сторон от знака равно стоят логарифмы с одним и тем же основанием, то приравниваем подлогарифмические выражения и решаем получившееся уравнение уже без логарифмов.
17. Если у логарифмов разные основания, то с помощью формул, приводим их к одному.
18. Если перед логарифмами есть коэффициенты, то поднимаем их как степень у подлогарифмического выражения.
19. Если логарифмов несколько, то с помощью формул превращаем их в один.
20. Показатель степени стоит наверху, над числом или над переменной. Основании степени стоит внизу.
21. Если в уравнении переменная находится в показателе степени, то нужно добиться того, чтобы с обеих сторон уравнения были одинаковые основания, после этого основания убираем и приравниваем только показатели степени.
22. При работе со степенными выражениями лучше избегать десятичных дробей.
23. Если переменная или выражение с переменной имеет степень (большую 1), а с другой стороны от знака равно есть число, то нужно представить это число в виде такой же степени, затем степени слева и справа от знака равно можно убрать.
24. Чтобы производить действия со степенями, основания должны быть одинаковыми. Чтобы основания стали одинаковыми можно числа раскладывать на множители (на слагаемые нельзя!), каждый из множитель получает такую же степень, как была у всего числа.
25. Если в степени находится разность чисел или переменных, то нужно перейти к делению оснований.
26. Если в степени находится сумма чисел или переменных, то нужно перейти к произведению оснований.
27. «Квадрат съедает квадратные корень». «Куб съедает кубические корень» и т.д.
28. Если у нескольких множителей есть одинаковая степень, то ее можно вынести за скобки.
Образцы решения
- В ходе распада радиоактивного изотопа его масса уменьшается по закону !!!, где m0 — начальная масса изотопа, t — время, прошедшее от начального момента, Т — период полураспада. В начальный момент времени масса изотопа 40 мг. Период его полураспада составляет 10 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг.
- Решение:
- подставляем все, что известно 5=40•2-t/10;
- упрощаем уравнение так, чтобы переменная осталась со своей стороны равенства в одиночестве;
- разделим обе части уравнения на 40: 5/40=2-t/10, то есть 1/8=2-t/10;
- так как в уравнении присутствует степень, добьемся того, чтобы слева и справа от знака равно стояли одинаковые основания: 2-3=2-t/10;
- основания одинаковые, можем их отбросить: -3=-t/10, то есть t=30;
- Ответ: 30.
- Решение:
- Зависимость объема спроса q (единицы в месяц) на продукцию предприятия-монополиста от цены р (тыс.руб. за ед.) задается формулой q=70-5р. Выручка предприятия r (в тыс. руб. за месяц) вычисляется по формуле r(р)=q•р. Определите наибольшую цену р, при которой месячная выручка r(р) составит не менее 240 тыс. рублей. Ответ приведите в тыс. руб. за ед.
- Решение:
- подставляем все, что известно 240≤(70-5р)•р, то есть 5р²-70р+240≤0;
- упростим неравенство — поделим все на 5 и решим квадратное уравнение р²-14р+48=0;
- р=6;8, то есть наибольшее р=8;
- Ответ: 8.
- Решение:
- Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы: Т(t)=T0+bt+at2, где t — время в минутах, T0=1200 К, а=-25 К/мин², b = 225 К/мин. Известно, что при температуре нагревательного элемента свыше 1400 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключать прибор. Ответ дайте в минутах.
- Решение:
- подставляем все, что известно 1400≤1200+225t-25t², то есть 25t²-225t+200≤0;
- упростим неравенство — поделим все на 25 и решим квадратное уравнение t²-9t+8=0;
- t=1;8, то есть через 1 минуту прибор уже выйдет из строя, остальные значения не имеют смысла, то есть наибольшее время работы 1 минута;
- Ответ: 1.
- Решение:
- Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объем и давление связаны соотношением р1V11,4=p2V21,4, где р1, р2 — давление газа (в атмосферах) в начальном и конечном состояниях, V1 и V2 — объем газа (в литрах) в начальном и конечном состояниях. Изначально объем газа равен 313,6 л, а давление газа равно одной атмосфере. До какого объема нужно сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах.
- Решение:
- подставляем в формулу все, что известно: 1•313,61,4=128•V21,4;
- запишем степени в виде неправильных дробей 1,4=14/10=7/5 и возведем обе части уравнения в обратную степень 5/7 (помним, что при возведении степени в степень, показатели степени перемножаются): (1•313,67/5)5/7=(128•V27/5)5/7;
- 313,6=1285/7•V2, 128=27, получим 313,6=(27)5/7•V2;
- 313,6=25•V2, 25=32, поэтому V2=313,6:32=9,8;
- Ответ: 9,8.
- Решение:
- Расстояние L (км), на котором виден горизонт, можно рассчитать по формуле !!!, где R — радиус Земли, равный 6400 км, h — высота (м) , на которой находится наблюдатель. Гуляющий по набережной ребенок видит линию горизонта на расстоянии 0,9 км. К набережной ведет спуск. На сколько ступенек ему нужно подняться, чтобы увидеть горизонт на расстоянии 4,1 км, если высота одной ступеньки 25 см.
- Решение:
- рассмотрим ситуацию, когда ребенок гуляет по набережной, тогда он видит горизонт на расстоянии !!!, отсюда можем найти h — высоту над уровнем моря, на которой находится набережная, h=405/6400 м;
- рассмотрим ситуацию, когда мальчик поднимется по ступенькам и будет видеть горизонт на расстоянии !!!, отсюда можем найти h — высоту над уровнем моря, на которую поднимется мальчик, h = 8405/6400 м;
- разница высот составляет 8405/6400-405/6400=8000/6400=80/64=10/8=5/4 м;
- количество ступенек = высота подъема/высота одной ступеньки= 5/4:0,25=5;
- Ответ: 5.
- Решение:
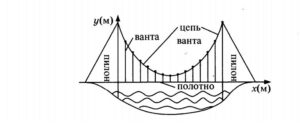
- Уравнение, описывающее характер провисания цепи вантового моста, имеет вид у=0,0024х²-0,24х+24. Найдите длину ванты, расположенной на расстоянии 20 м от пилонов, х и у измеряются в метрах. Ответ дайте в метрах.
- Решение:
- 20 м от пилона — это координата х, подставляем в заданное уравнение все, что известно:
- у=0,0024•20²-0,24•20+24= 20,16;
- 20 м от пилона — это координата х, подставляем в заданное уравнение все, что известно:
- Ответ: 20,16.
- Решение:
- Эффективную температуру звезд можно рассчитать по формуле Р=σST4. Известно, что площадь поверхности некоторой звезды S = 1021/256 (м2), постоянная σ=5,7•10-8, излучаемая звездой мощность Р=5,7•1025 Вт. Найдите температуру этой звезды.
- Решение:
- подставим в формулу все, что известно: !!!
- Ответ: 4000.
- Решение:
- Расстояния от линзы до предмета и от линзы до экрана связаны соотношением !!!, где фокусное расстояние f=28 см, расстояние от линзы до предмета d1 может меняться от 40 до 60 см, расстояние от линзы до экрана d2 — от 53 см до 77 см. На каком наименьшем расстоянии от линзы можно разместить предмет, чтобы его изображение было четким. Ответ дайте в см.
- Решение:
- пусть изображение получается на расстоянии 53 см, тогда !!!, то есть d1=59,36;
- пусть изображение получается на расстоянии 77 см, тогда!!! , то есть d1=44;
- во втором случае d1 меньше;
- Ответ: 44.
Формулы с дробями
- Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость погружения батискафа вычисляется по формуле
где
м/с — скорость звука в воде,
— частота испускаемых импульсов,
— частота отражённого от дна сигнала, регистрируемая приёмником (в МГц). Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 2 м/с. Ответ: 751. (Демонстрационная версия-2021)
- Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой
где
– температура нагревателя (в градусах Кельвина),
– температура холодильника (в градусах Кельвина). При какой температуре нагревателя
КПД этого двигателя будет
если температура холодильника
К? Ответ выразите в градусах Кельвина. Ответ: 420. (Досрочная волна-2021)
- В розетку электросети подключены приборы, общее сопротивление которых составляет
Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление
этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями
Ом и
Ом их общее сопротивление даeтся формулой
(Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в омах. Ответ: 10. (Основная волна-2021)
- К источнику с ЭДС
и внутренним сопротивлением
хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, задаётся формулой
При каком наименьшем значении сопротивления нагрузки напряжение на ней будет не менее 120 В? Ответ выразите в Ом. Ответ: 12(Основная волна.2019)
- Рейтинг
интернет-магазина вычисляется по формуле
— средняя оценка магазина покупателями,
— оценка магазина, данная экспертами,
— число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 26, их средняя оценка равна 0,68, а оценка экспертов равна 0,23. Ответ: 0,63(Основная волна.2014)
- Автомобиль, движущийся в начальный момент времени со скоростью v0 =15 м/с, начал торможение с постоянным ускорением a = 2 м/с2 . За t секунд после начала торможения он прошёл путь
(м).Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 36 метров. Ответ выразите в секундах. Ответ: 3(Досрочная волна.2014)
- Независимое агентство намерено ввести рейтинг R новостных изданий на основе показателей информативности In, оперативности Op и объективности Tr публикаций. Каждый показатель оценивается целыми числами от −1 до 1. Аналитик, составляющий формулу, считает, что объективность публикаций ценится втрое, а информативность — вчетверо дороже, чем оперативность. В результате формула примет вид
Формулы со степенями
- Два тела, массой m = 9 кг каждое, движутся с одинаковой скоростью v = 6 м/c под углом 2α друг к другу. Энергия (в Дж), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле Q=mv²sin²α, где m — масса (в кг), \upsilon — скорость (в м/с). Найдите, под каким углом 2α должны двигаться тела, чтобы в результате соударения выделилась энергия, равная 81 Дж. Ответ дайте в градусах. Ответ: 60(Досрочная волна.2020)
- Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объём и давление связаны соотношением
где
и
— давление газа (в атмосферах) в начальном и конечном состояниях,
и
— объём газа (в литрах) в начальном и конечном состояниях. Изначально объём газа равен 256 л, а давление газа равно одной атмосфере. До какого объёма нужно сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах. Ответ: 8 (Досрочная волна. 2019)
- При адиабатическом процессе для идеального газа выполняется закон
где p — давление в газа (в Па), V — объём газа (в м3),
Найдите, какой объём V (в м3) будет занимать газ при давлении p, равном 2·105 Па. Ответ: 125(Досрочная волна.2019)
- Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому
где P — мощность излучения звезды (в ваттах),
— постоянная, S — площадь поверхности звезды (в квадратных метрах), а
— температура (в кельвинах). Известно, что площадь поверхности некоторой звезды равна
м2, а мощность её излучения равна
Вт. Найдите температуру этой звезды в кельвинах. Ответ: 3000(Досрочная волна.2019)
Формулы с корнями
- Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением a км/ч 2. Скорость вычисляется по формуле
где l — пройденный автомобилем путь. Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав 0,5 километра, приобрести скорость 80 км/ч. Ответ выразите в км/ч2. Ответ: 6400 (Основная волна.2020)
- Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением
Скорость
(в км/ч) вычисляется по формуле
где
— пройденный автомобилем путь (в км). Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 90 км/ч. Ответ: 0,9 (Досрочная волна.2016)
Формулы с логарифмами
- Водолазный колокол, содержащий
моль воздуха при давлении
атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления
Работа, совершаемая водой при сжатии воздуха, определяется выражением
где
— постоянная,
К — температура воздуха. Найдите, какое давление
(в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 29100 Дж. Ответ: 7. (Досрочная волна.2018)
- Ёмкость высоковольтного конденсатора в телевизоре
Параллельно с конденсатором подключён резистор с сопротивлением
Во время работы телевизора напряжение на конденсаторе
После выключения телевизора напряжение на конденсаторе убывает до значения
за время, определяемое выражением
где
— постоянная. Определите наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 16,2 с. Ответ дайте в кВ (киловольтах). Ответ: 6(Досрочная волна.2013)
Формулы с квадратными уравнениями
- Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в К) от времени работы:
где t — время (в мин.), T0 = 1380 К, a = −15 К/мин2, b = 165 К/мин. Известно, что при температуре нагревательного элемента свыше 1800 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах. Ответ: 4. (Досрочная волна.2017)