ЕГЭ-математика-профиль-задание 17

Алгоритм (работает для всех типов задач)

1шаг (всегда) Записать ограничения. Ограничения есть, если

• в задании есть дробь, в знаменателе которой есть переменная. Выписываем знаменатель (весь), он не может быть равен нулю. Находим запрещенные х.
• в задании есть логарифм. Выписываем подлогарифмическое выражение (если в нем есть переменная), оно должно быть строго больше нуля. Выписываем основание (если в нем есть переменная), оно должно быть строго больше нуля и не равно 1. Решаем получившиеся неравенства (все), находим допустимые промежутки, обобщаем результат.
• в задании есть корень. Выписываем подкоренное выражение (все; без корня), оно должно быть больше или равно нулю. Находим промежуток с допустимыми значениями х.
• если в задании несколько ограничений, то рассматриваем все и обобщаем результат, чаще всего это делается на координатной прямой.
• в тексте решения оформляем так: «Решим … (уравнение, неравенство, систему) при условии, что ….

2шаг. Упростить заданные уравнения, неравенства или системы. Какие могут быть использованы упрощения:

• приводим заданное выражение к квадратному;
• исследуем дискриминант;
• используем свойства параболы;
• используем замену;
• выносим общий множитель за скобки;
• решаем распадающееся уравнение;
• решаем систему способом подстановки;
• решаем систему способом сложения, вычитания;
• приводим к стандартному виду окружности;
• используем свойства окружности;
• исследуем функцию с помощью производной;
• используем свойства тригонометрических функций;
• применяем формулы сокращенного умножения;
• применяем тригонометрические формулы;
• раскрываем модуль;
• используем формулы логарифмов;
• Вы должны самостоятельно, без подсказок в задании, увидеть, что можно упростить в задании и какое из правил применить;
• сообщать в решении о том, что Вы сейчас проводите упрощения не надо;

3шаг. Решаем упрощенное уравнение или неравенство. Как правило, это самая легкая часть задания.

4 шаг. Проверяем найденные корни на соответствие ограничениям и условию задачи. Просто не забудьте этот шаг, выполняется он легко.

5 шаг. Наносим все найденные решения и ограничения на общую координатную прямую. Отмечаем на ней количество решения на каждом интервале и в отмеченных точках. Записываем обобщенный результат. Очень ответственный шаг, пожалуй, самый сложный в этом задании.

Алгоритм и образцы решения заданий с корнями

1. Если в задании есть корни, то я сразу выписываю ограничения: подкоренное выражение должно быть больше или равно 0.

2. Если я вижу, что в уравнении вся правая (или левая) часть стоит под корнем, то я возвожу обе части уравнения в квадрат.

3. Если я вижу в задании, что в одной части уравнения есть корень, а в другой нет, то я ввожу ограничения на ту часть, что не содержит корня. Она должна быть больше или равна 0. Запись такого решения оформляю в виде системы: первое неравенство – это ограничение для той части, что не содержит корня; второе уравнение – заданное уравнение, которое уже возвели в квадрат (освободились от корня).

---

1.

---

2.

---

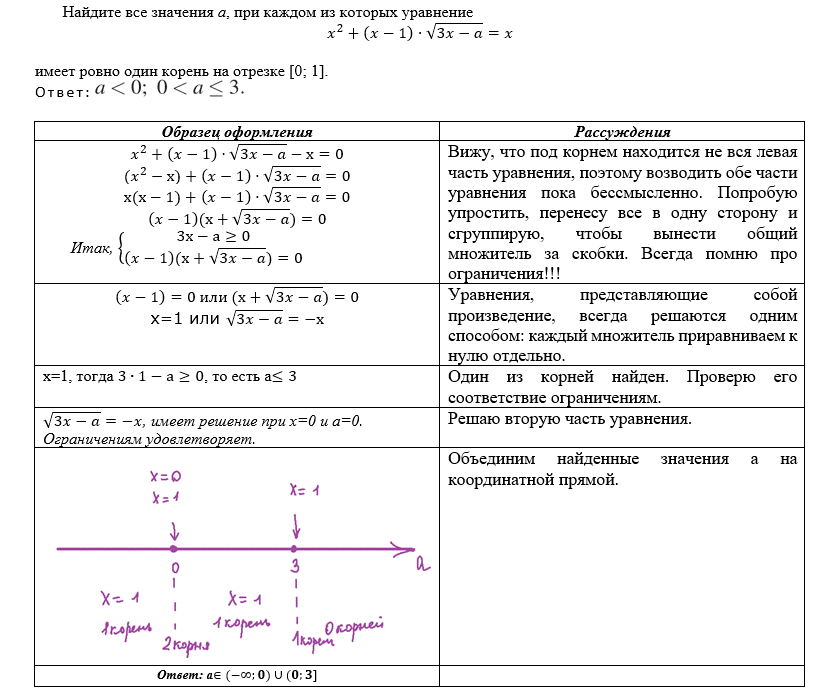
3.

---

Образцы решений составлены по заданиям из реальных ЕГЭ 2016-2020 гг. Если Вы сами не смогли решить задачу, то ВЫУЧИТЕ представленное решение, а не просто просмотрите или спишите его.

1. (2020 г.) Найдите все значения параметра а, при каждом из которых система  (!!!) имеет ровно два различных решения.

Размышления: оба уравнения содержат две переменные в квадрате, такое сочетание мы встречаем в уравнениях окружности, поэтому попробуем привести оба уравнения к стандартному виду окружности: (х-х₀)²+(у-у)₀)²=r², где (х0;у0) — центр окружности; r — радиус окружности.

Записываем в решении: приведем заданные уравнения к стандартному уравнению окружности:

(1) х2+в2-2x-2u=0 (х2-2x)+(у2-2u)=0 /сформируем квадраты разности/ (х2-2x•1+1-1)+(у2-2u•1+1-1)=0 (х2-2x•1+1)-1+(u)2-2u•1+1)-1=0 (х-1)2+(у-1)2-2=0 (х-1)2+(у-1)2=2 Это окружность с центром (1;1) и радиусом √2.

(2) х2+в2-2(1+а)ч-2(1-а)у=-2а2 (х2-2(1+а)х)+(у2-2(1-а)у)=-2а2 /сформируем квадраты разности/ (х2-2(1+а)х+(1+а)2-(1+а)2)+(в2-2(1-а)у+(1-а)2-(1-а)2)=-2а2 (х2-2(1+а)х+(1+а)2)-(1+а)2+(у2-2(1-а)у+(1-а)2)-(1-а)2=-2а2 (х-1-а)2+(у-1-а)2-2-2а2=-2а2 (х-1-а)2+(у-1-а)2=2+2а2-2а2 (х-1-а)2+(u-1+a)2=2 Это окружность с центром (1+а;1-а) и радиусом √2.

Размышления: в задании сказано, что решений должно быть «ровно два различных». Количество решений зависит от расположения окружностей.

• Если центры окружностей совпадут, то и окружности совпадут, и решений будет бесконечно много, что нам не подходит. Эта ситуация нам не нужна, поэтому нужно вычислить а, при которых это произойдет, чтобы это значение исключить из ответа. 
• Если окружности касаются, то между их центрами расстояние равное сумме двух радиусов, тогда имеется одно решение, нам это не подходит. Обязательно нужно найти а, при которых эта ситуация возникает, чтобы исключить из ответа.
• Если расстояние между окружностями больше суммы их радиусов, то окружности не пересекаются и не касаются. Пересечение возможно, если расстояние меньше суммы радиусов.

Чтобы найти расстояние между центрами, достроим прямоугольный треугольник и воспользуемся теоремой Пифагора. Гипотенуза — это сумма двух радиусов; горизонтальный катет равен разности абсцисс центров окружностей, вертикальный катет — это разность ординат центров окружностей.

Записываем в решение: рассмотрим различные расположения окружностей друг относительно друга:

• центры окружностей совпадают:

a=0

• окружности касаются: (√2+√2)²=(1+a-1)²+(1-1+a)²

8=2a², то есть а=±2.

• При а от -2 до 2 наши окружности пересекаются, то есть имеется 2 решения, но при а=0 этих решений бесконечно много, поэтому окончательный ответ: (-2;0)∪(0;2)

2. (2020 г.) Найдите все значения параметра а, при каждом из которых уравнение

имеет единственное решение.

Размышления: ужасное уравнение, с обеих сторон есть корни, то есть в квадрат возводить бесполезно, он останется. Везде есть а.  И есть ограничения, обязательно начну в них, а потом буду упрощать. Надо хотя бы одну часть уравнения сделать проще, убрать оттуда а, пусть там будут только числа и х: (записываем в решении)

• Решим уравнение при условии, что

то есть 1≤а≤5.

Больше упростить не получается, разобьем уравнение на две функции: (записываем)

Пусть

Уравнения содержат две переменные в квадрате, что наводит на мысль о том, что это окружность, приведем этой уравнение к стандартному виду окружности (х-х₀)²+(у-у₀)²=r², где (х0;у0) — центр окружности; r — радиус окружности.:

Исследуем первую функцию: оставим корень справа  в одиночестве возведем обе части уравнения в квадрат при условии, что у+3≥0, то есть у≥-3 (то есть это полуокружность, верхняя часть окружности) (х2-6х)+(у2+6у)=-17 /приведем скобки к квадрату разности/ (х2-2•3х+9-9)+(у2+2•3у+9-9)=-17 (х2-2•3х+9)-9+(у2+2•3у+9)-9=-17 (х-3)2-9+(у+3)2-9=-17 (х-3)2-9+(у+3)2-9=1 Это полуокружность окружность с центром (3;-3) и радиусом 1.

Исследуем вторую функцию: оставим корень справа  в одиночестве возведем обе части уравнения в квадрат при условии, что y+a≥0, то есть y≥-a (то есть это полуокружность, верхняя часть окружности) y2+2ay+a2=1+2ax-a2-x2 (x2-2ах)+(у2+2ay)=1-2a2 (x2-2ах+а2-а2)+(у2+2ay+а2-а2)=1-2a2 (x2-2ах+а2)-а2+(у2+2ay+а2)-а2=1-2a2 (x-а)2-а2+(у+а)2-а2=1-2a2 (x-а)2+(у+а)2=1 Это полуокружность с центром (а;-а) и радиусом 1. А могут быть и дробными, количество полуокружностей бесконечно, но для понимания их расположения достаточно этих.

Рассмотрим различные расположения полуокружностей:

• пусть их центры совпадают, тогда и сами полуокружности совпадают, то есть бесконечно много решений — не подходит, значение а, при котором это происходит необходимо исключить из ответа. Условие совпадения центров:

3=а и -3=-а, то есть а=3 (исключить).

• полуокружности должны иметь общие точки, поэтому два крайних положения второй полуокружности нам уже не подходят, нам необходимы полуокружности с а=2 и 4 и все, что находятся между ними:

То есть а∈[2;3)∪(3;4].

3. (2020 г.) Найдите все значения параметра а, при каждом из которых уравнение х⁴sinα+2x²cosα+sinα=0 имеет ровно 2 различных решения.

Размышления: это биквадратное уравнение, буду вводить замену; здесь две тригонометрические функции-надо упростить, поделю все на sinα: (записываем в решении)

• х⁴sinα+2x²cosα+sinα=0 /: sinα, sinα≠0, α≠πn,n∈Z

х⁴+2x²ctgα+1=0/ замена: t=x²,t >0 (t≠0, так как будет только один корень, а это противоречит условию задачи)

t²+2tctgα+1=0 / D=4ctg²α-4 , так как каждая t для х означает два корня, то нам нужна только одна t, то есть D должен быть равен 0:

4ctg²α-4=0, то есть ctgα=1 и ctgα=-1. Нам нужно убедиться, что t получится положительным, поэтому подставим найденные значения ctgα и найдем t.

При ctgα=1 t=-1 — не подходит; при ctgα=-1 t=1 — удовлетворяет ограничениям, так как даст два различных значения х.

• Найдем α, при котором ctgα=-1. α=-π/4+πn, n∈Z.

4. (2020 г.) Найдите все значения параметра а, при каждом из которых уравнение

имеет ровно 2 различных решения.

Размышления: в знаменателе есть переменные=требуется рассмотреть ограничения; затем нужно найти нули дроби (приравнять числитель к 0) и проверить найденные корни на ограничения и на совпадение (так как нужно два различных корня).

Записываем решение:

• Решим уравнение при условии, что х²+8х+16-а²≠0.
• Найдем х, при которых дробь превращается в 0:

9х²-а²=0, то есть х=а/3 и х=-а/3

• найдем а, при которых эти корни совпадают /приравняем корни/: а/3=-а/3, то есть а=0. Это решение нам не подходит, так как необходимы 2 различных корня. Его нужно исключить из ответа.
• проверим найденные корни на соответствие ограничениям /подставим х в ограничения и найдем а:

при х=а/3:

а≠6, а≠-3

при х=-а/3

а≠-6, а≠3

Обобщим найденные решения: а∈(-∞;-6)∪(-6;-3)∪(-3;0) ∪(0;3) ∪(3;6)∪(6;+∞).

5. (2019 г.) Найдите все значения параметра а, при каждом из которых наименьшее значение функции

f(x)=x-2|x|+|x²-2(a+1)x+a²+2a|

больше -4.

Размышления: первая мысль «Фу, модуль» быстро пролетает мимо, не тратим на нее время! По условию задачи все это выражение должно быть больше -4, так и перепишем его, а еще разместим модули по разные стороны от знака неравенства, чтобы получить два выражения попроще.

Пишем: x-2|x|+|x²-2(a+1)x+a²+2a|>-4

|x²-2(a+1)x+a²+2a|>2|x|-х-4

Левую и правую части неравенства рассмотрим отдельно.

Левая часть — это модуль квадратичной функции, графиком которой является парабола ветвями вверх (так как коэффициент перед x²>0, средняя часть параболы «отзеркалена» вверх относительно оси ОХ (так как есть модуль). Эта парабола перемещается вдоль оси ОХ при а>0 направо, при а<0 налево. Вершина параболы (а+1;1).

Правая часть представляет собой прямую у=х-4 (при х≥0), проходящую через I и III четверти и пересекающую ось ОХ в точке 4, а ОУ в точке -4; при х<0 у=4-3х, проходящую через II  и IV четверти и пересекающую ось ОХ в точке -4/3, а ОУ в точке -4.

Нас интересует такое расположение параболы, чтобы

• точки ее пересечения с ОХ были между точками пересечения прямых с ОХ,
• правая ветвь правой параболы была выше прямой у=х-4;
• левая ветвь левой параболы выше прямой у=-4-3х:

Найдем а, при которых выполняются эти условия:

• пересечение параболы с ОХ: x²-2(a+1)x+a²+2a=0 

Координата правой точки пересечения параболы с ОХ а+2 должна быть меньше или равна 4, то есть а≤2.

Координата левой точки пересечения параболы с ОХ а должна быть больше или равна -4/3, то есть а≥-4/3.

• найдем условия размещения параболы выше прямых:

правая ветвь параболы должна быть выше прямой у=х-4 x2-2(a+1)x+a2+2a>x-4 x2-2(a+1)x+a2+2a-х+4>0 /представим квадратное выражение в стандартном виде/ x2-(2a+3)x+a2+2a+4>0 при а≥/7/4. Точка касания справа должна удовлетворять условию 4a2-24a+32≤0 Найдем а, при которых выражение превращается в 0: а2-6а+8=0 При а=2 и а=4 выражение обращается в 0. Исследуем его знаки с учетом ограничения: то есть единственное подходящее всем ограничениям решение а=2

левая ветвь параболы должна быть выше прямой у=-3х-4 x2-2(a+1)x+a2+2a>4-3х x2-2(a+1)x+a2+2a+3х-4>0 /представим квадратное выражение в стандартном виде/ x2-(2a-1)x+a2+2a+4>0 Точка касания слева должна удовлетворять условию 9(-12a-15)≤25+60a+36a2 36a2+168a+160≥0 Найдем а, при которых выражение превращается в 0: 9а2+42а+40=0 При а=-10/3 и а=-4/3 выражение обращается в 0. Исследуем его знаки с учетом ограничения: При а∈[-4/3;-1,25) существует 2 корня, то есть парабола и прямая у=-3х-4 пересекаются, то есть часть параболы находится под прямой, а это противоречит условию задачи. Нас интересует только касание, а это возможно только при а=-1,25 (D=0)

При всех а от -1,25 до 2 парабола находится выше прямых, поэтому ответ: -1,25<а<2.