ЕГЭ-математика-профиль-задание-8

Задачи на сплавы и растворы

Правила. Алгоритм. Образец решения.

1. Такие задачи решаются с помощью уравнения. Неизвестные величины обозначаем переменными, их может быть несколько.

2. После чтения условия обязательно нужно ответить для себя на следующие вопросы:

сколько растворов (или сплавов) участвует в задаче;
какова масса (или объем) и концентрация каждого раствора.

3. Если в задаче говорится о том, что смешали 2 раствора, то всего в задаче участвуют 3 раствора. Третий раствор — это итоговый раствор, который получается в результате спешивания.

4. Значение концентрации используем без процентов. Для этого данное в задаче значение нужно поделить на 100.

5. Масса итогового сплава (или раствора) равна сумме масс первого и второго сплава (или раствора).

6. Концентрацию итогового сплава или раствора НЕЛЬЗЯ находить как сумму концентраций первого и второго сплава.

7. Концентрация кислоты в воде = 0.

8. Фраза «такой же массы» означает, что массу и первого, и второго растворов обозначаем m (или х).

9. После решения уравнения обязательно проверьте, ответили ли Вы на вопрос задачи или требуются дополнительные действия.

[свернуть]

Алгоритм

1. Для каждой такой задачи составляем схему:

Первый раствор (сплав):

масса = …
концентрация = …
умножаем массу на концентрацию = … (результат 1)

Второй раствор (сплав):

масса = …
концентрация = …
умножаем массу на концентрацию = … (результат 2)

Итоговый раствор (сплав):

масса = …
концентрация = …
умножаем массу на концентрацию = … (результат 3)

Составляем уравнение: результат 1 + результат 2 = результат 3.

Осталось решить уравнение.

2. Если в задаче идет речь о трех или четырех сплавах (или растворах), то количество участников уравнения просто увеличивается.

3. Если в задаче описывается несколько опытов, то подобную схему расписываем для каждого опыта отдельно. Тогда задача решается системой уравнений.

[свернуть]

Образцы решения

№ 1

Условие: В одном сосуде содержится 6 литров 13-процентного водного раствора некоторого вещества, а во втором — 7 литров воды. Сколько процентов составит концентрация раствора, который получится, если смешать раствор и воду?

Рассуждения и вычисления:

1. Составляем схему:

Первый раствор:

масса = 6
концентрация = 0,13
умножаем массу на концентрацию = 6•0,13=0,78

Второй раствор:

масса = 7
концентрация = 0
умножаем массу на концентрацию = 7•0=0

Итоговый раствор:

масса = 6+7=13
концентрация = х
умножаем массу на концентрацию = 13х

Составляем уравнение: 0,78+0=13х.

Решаем уравнение: х= 0,06, то есть концентрация итогового раствора 6%.

Ответ: 6.

№ 2

Условие: Смешали 10-процентный раствор некоторого вещества с 18-процентным раствором вещества такой же массы. Сколько процентов составляет концентрация получившегося раствора?

Рассуждения и вычисления:

1. Составляем схему:

Первый раствор:

масса = х
концентрация = 0,1
умножаем массу на концентрацию = 0,1х

Второй раствор:

масса = х
концентрация = 0,18
умножаем массу на концентрацию = 0,18х

Итоговый раствор:

масса = х+х=2х
концентрация = y
умножаем массу на концентрацию = 2хy

Составляем уравнение: 0,1x+0,18x=2хy.

Решаем уравнение: y = 0,14, то есть концентрация итогового раствора 14%.

Ответ: 14.

№ 3

Условие: Из двух сплавов, один из которых содержит 20% никеля, а второй — 40% никеля, получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса второго сплава меньше массы первого?

Рассуждения и вычисления:

1. Составляем схему:

Первый сплав:

масса = х
концентрация = 0,2
умножаем массу на концентрацию = 0,2х

Второй сплав:

масса = 200-х
концентрация = 0,4
умножаем массу на концентрацию = (200-х)•0,4

Итоговый сплав:

масса = 200
концентрация = 0,25
умножаем массу на концентрацию = 200•0,25=50

Составляем уравнение: 0,2x+(200-x)•0,4=50.

Решаем уравнение: х = 150, то есть масса первого сплава 150 кг. Это не ответ на вопрос задачи.

Найдем массу второго сплава: 200-150=50. Это не ответ на вопрос задачи.

Найдем разницу в массах сплавов: 150-50=100.

Ответ: 100.

№ 4

Условие: Первый сплав содержит 10% меди, второй — 30% меди. Масса второго сплава больше массы первого на 2 кг. Из этих двух сплавов получили третий сплав, содержащий 25% меди. Найдите массу третьего сплава.

Рассуждения и вычисления:

1. Составляем схему:

Первый сплав:

масса = х
концентрация = 0,1
умножаем массу на концентрацию = 0,1х

Второй сплав:

масса = х+2
концентрация = 0,3
умножаем массу на концентрацию = (х+2)•0,3

Итоговый сплав:

масса = х+х+2=2х+2
концентрация = 0,25
умножаем массу на концентрацию = (2х+2)•0,25

Составляем уравнение: 0,1x+(х+2)•0,3=(2х+2)•0,25.

Решаем уравнение: х = 1, то есть масса первого сплава 1 кг. Это не ответ на вопрос задачи.

Найдем массу итогового сплава: 2•1+2=4.

Ответ: 4.

№ 5

Условие: Смешав 40-процентный и 60-процентный растворы кислоты и добавив 100 кг чистой воды, получили 24-процентный раствор кислоты. Если бы вместо 100 кг воды добавили 100 кг 52-процентного раствор такой же кислоты, то получили бы 50-процентный раствор кислоты. Сколько килограммов 40-процентного раствора кислоты использовали для получения смеси?

Рассуждения и вычисления:

*В это задаче проводится два опыта, поэтому схему составляем дважды и решаем систему уравнений.

** В каждом опыте участвуют 4 раствора (три смешивают и получают итоговый раствор).

1. Составляем схему первого опыта:

Первый раствор:

масса = х
концентрация = 0,4
умножаем массу на концентрацию = 0,4х

Второй раствор:

масса = y
концентрация = 0,6
умножаем массу на концентрацию = 0,6y

Третий раствор:

масса = 100
концентрация = 0
умножаем массу на концентрацию = 0

Итоговый раствор:

масса = х+y+100
концентрация = 0,24
умножаем массу на концентрацию = (х+y+100)•0,24

Составляем уравнение: 0,4x+0,6y+0=(х+y+100)•0,24.

Можем упростить: 4x+9y=600.

2. Составляем схему второго опыта:

Первый раствор:

масса = х
концентрация = 0,4
умножаем массу на концентрацию = 0,4х

Второй раствор:

масса = y
концентрация = 0,6
умножаем массу на концентрацию = 0,6y

Третий раствор:

масса = 100
концентрация = 0,52
умножаем массу на концентрацию = 100•0,52=52

Итоговый раствор:

масса = х+y+100
концентрация = 0,5
умножаем массу на концентрацию = (х+y+100)•0,5

Составляем уравнение: 0,4x+0,6y+52=(х+y+100)•0,5.

Можем упростить: x-y=20.

3. Составляем систему уравнений:

4x+9y=600
x-y=20

Решаем систему любым способом. Находим х = 60, то есть масса первого раствора 60 кг.

Ответ: 60.

№ 6

Условие: Имеются два сосуда. Первый содержит 20 кг, а второй — 10 кг кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 48% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 50% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

Рассуждения и вычисления:

*В это задаче проводится два опыта, поэтому схему составляем дважды и решаем систему уравнений.

1. Составляем схему первого опыта:

Первый раствор:

масса = 20
концентрация = х
умножаем массу на концентрацию = 20х

Второй раствор:

масса = 10
концентрация = y
умножаем массу на концентрацию = 10y

Итоговый раствор:

масса = 20+10=30
концентрация = 0,48
умножаем массу на концентрацию = 30•0,48=14,4

Составляем уравнение: 20x+10y=14,4.

Можем упростить: 2x+y=1,44.

2. Составляем схему второго опыта:

Первый раствор:

масса = z
концентрация = x
умножаем массу на концентрацию = хz

Второй раствор:

масса = z
концентрация = y
умножаем массу на концентрацию = yz

Итоговый раствор:

масса = z+z=2z
концентрация = 0,5
умножаем массу на концентрацию = 2z•0,5=z

Составляем уравнение: xz+yz=z.

Можем упростить: x+y=1.

3. Составляем систему уравнений:

2x+y=1,44
x+y=1

Решаем систему любым способом. Находим х = 0,44, то есть концентрация первого раствора 44 %. Это не ответ на вопрос задачи.

Масса первого раствора по условию составляет 20 кг. 44% от этой массы составляет кислота. Составим пропорцию:

20 кг — 100%
m — 44%

Решаем пропорцию любым способом, получаем, что m=8,8 кг.

Ответ: 8,8.

№ 7

Условие: Сушеный виноград — это изюм. Сколько килограммов винограда потребуется для получения 10 кг изюма, если виноград содержит 90% воды, а изюм содержит 20%?

Рассуждения и вычисления:

1. И свежий виноград и изюм, кроме воды, содержат мякоть. Количество мякоти в них одинаково. (информация не относящаяся к математике, но необходимая для решения задачи).

2. Свежий виноград:

общая масса — х
концентрация воды — 0,9х
концентрация мякоти 0,1х

3. Изюм:

общая масса — 10 кг
концентрация воды — 0,2 от 10 кг
концентрация мякоти — 0,8 от 10 кг, то есть 0,8•10=8 кг

4. Так как масса мякоти одинакова и в свежем винограде, и в изюме, то

концентрация мякоти в винограде = концентрации мякоти в изюме, то есть 01,х=8
отсюда х=80 кг.

Ответ: 80.

[свернуть]

Задачи для тренировки

1. В сосуд, содержащий 9 литров 10-процентного водного раствора вещества, добавили 6 литров воды. Сколько процентов составляет концентрация получившегося раствора?

2. В сосуд, содержащий 6 литров 30-процентного водного раствора вещества, добавили 4 литра воды. Сколько процентов составляет концентрация получившегося раствора?

3. В сосуд, содержащий 9 литров 35-процентного раствора вещества, добавили 11 литров 15-процентного раствора. Сколько процентов составляет концентрация получившегося раствора?

4. В сосуд, содержащий 7 литров 25-процентного водного раствора вещества, добавили 8 литров 10-процентного раствора. Сколько процентов составляет концентрация получившегося раствора?

5. В сосуд, содержащий 6 литров 35-процентного водного раствора вещества, добавили 9 литров 30-процентного раствора. Сколько процентов составляет концентрация получившегося раствора?

6. В сосуд, содержащий 9 литров 20-процентного водного раствора вещества, добавили 11 литров 40-процентного раствора. Сколько процентов составляет концентрация получившегося раствора?

7. В сосуд, содержащий 3 литра 30-процентного водного раствора вещества, добавили 7 литров 10-процентного раствора. Сколько процентов составляет концентрация получившегося раствора?

8. Имеется два сплава. Первый содержит 35% никеля, второй — 50% никеля. Из этих двух сплавов получили третий, содержащий 45% никеля. Масса первого сплава равна 35 кг. На сколько масса первого сплава меньше массы второго?

9. Имеется два сплава. Первый содержит 45% никеля, второй — 5% никеля. Из этих двух сплавов получили третий, содержащий 15% никеля. Масса первого сплава равна 40 кг. На сколько масса первого сплава меньше массы второго?

10. В сосуд, содержащий 5 литров 16-процентного водного раствора вещества, добавили 3 литра воды. Сколько процентов составляет концентрация получившегося раствора?

11. Имеется два сплава. Первый содержит 10% никеля, второй — 45% никеля. Из этих двух сплавов получили третий, содержащий 35% никеля. Масса первого сплава равна 60 кг. На сколько масса первого сплава меньше массы второго?

[свернуть]

Задачи на нахождение средней скорости

Правила

1. Средняя скорость рассчитывается по формуле 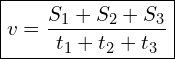$\boxed{v=\frac{S_1+S_2+S_3}{t_1+t_2+t_3}}$ .

нужно сложить все отрезки пути и поделить на сумму всех отрезков времени.

2. Если не известны отдельные отрезки пути, то найдите их по формуле $\boxed{S=vt}$ .

3. Если не известны отдельные отрезки времени, то найдите их по формуле 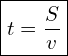$\boxed{t=\frac{S}{v}}$ .

4. Найти среднюю скорость движение — это не тоже самое, что найти среднее арифметическое. Если в задании даны значения скоростей на отдельных участках, то их нельзя складывать и делить на их количество. Это неправильно!

5. Фраза в условии задачи «половина пути» может быть записана как 0,5S, фраза «треть пути» — $\frac{S}{3}$ .

6. Фраза в условии задачи «половина времени» может быть записана как 0,5t, фраза «треть времени» — $\frac{t}{3}$ .

7. Фраза в условии задачи «обратный путь» означает, что путь и туда и обратно равен S.

8. Внимательно контролируйте единицы измерения, при необходимости выполните перевод:

если расстояние измеряется в километрах, то время в часах, а скорость в км/ч;
если расстояние измеряется в метрах, то время в секундах, а скорость в м/с.

[свернуть]

Алгоритм

1. Выпишите все известные величины из задачи.

2. Неизвестные величины найдите или выразите их через переменные (буквы).

3. Подставьте все данные (числовые и буквенные) в основную формулу для средней скорости.

4. Упростите полученное выражение (выполните сложение, приведите к общему знаменателю, избавьтесь от многоэтажных дробей, сократите).

5. Выпишите в ответ только числовое значение.

6. Если в ответе не получается целое число или конечная десятичная дробь, то задачу Вы решили не верно, нужно переделать.

[свернуть]

Образец решения

Условие: первую треть трассы автомобиль ехал со скоростью 30 км/ч, вторую треть — со скоростью 130 км/ч, а последнюю — со скоростью 60 км/ч. Найдите среднюю скорость автомобиля. Ответ дайте в км/ч.

Рассуждения и вычисления:

1. Для формулы средней скорости необходимо знать S_1, S₂, S₃. Расстояние мне не известно. Обозначу весь путь как S, тогда

$S_1=\frac{S}{3}$ , $S_2=\frac{S}{3}$ , $S_3=\frac{S}{3}$ .

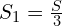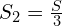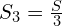2. Для формулы средней скорости необходимо знать t₁, t₂, t₃. Время мне не известно. Найду время движения на каждом участке по формуле 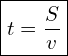$\boxed{t=\frac{S}{v}}$ :

$t_1=\frac{S_1}{30}=\frac{\frac{S}{3}}{30}=\frac{S}{90}$ , $t_2=\frac{S_2}{130}=\frac{\frac{S}{3}}{130}=\frac{S}{390}$ , $t_3=\frac{S_3}{60}=\frac{\frac{S}{3}}{60}=\frac{S}{180}$ .

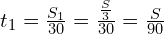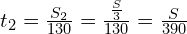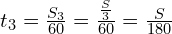3. Подставляю все найденные и выраженные величины в основную формулу:

$v=\frac{S_1+S_2+S_3}{t_1+t_2+t_3}=\frac{\frac{S}{3}+\frac{S}{3}+\frac{S}{3}}{\frac{S}{90}+\frac{S}{390}+\frac{S}{180}}=\frac{S}{\frac{26S}{2340}+\frac{6S}{2340}+\frac{13S}{2340}}=\frac{S}{\frac{S}{52}}=52$ .

4. Ответ: 52.

[свернуть]

Задачи для тренировки

1. Первую треть пути поезд прошел со скоростью 30 км/ч, вторую треть — со скоростью 150 км/ч, а последнюю — со скоростью 100 км/ч. Найдите среднюю скорость, ответ дайте в км/ч.

2. Первую треть пути поезд прошел со скоростью 60 км/ч, вторую треть — со скоростью 120 км/ч, а последнюю — со скоростью 110 км/ч. Найдите среднюю скорость, ответ дайте в км/ч.

3. Путешественник переплыл море на яхте со средней скоростью 14 км/ч. Обратно он летел на спортивном самолете со скоростью 378 км/ч. Найдите среднюю скорость движения.

4. Путешественник переплыл море на яхте со средней скоростью 13 км/ч. Обратно он летел на спортивном самолете со скоростью 325 км/ч. Найдите среднюю скорость движения.

5. Путешественник переплыл море на яхте со средней скоростью 12 км/ч. Обратно он летел на спортивном самолете со скоростью 276 км/ч. Найдите среднюю скорость движения.

6. Первые 110 км поезд прошел со скоростью 60 км/ч, следующие 100 км — со скоростью 90 км/ч, а затем 150 км — со скоростью 100 км/ч. Найдите среднюю скорость, ответ дайте в км/ч.

7. Первые 140 км поезд прошел со скоростью 50 км/ч, следующие 160 км — со скоростью 60 км/ч, а затем 120 км — со скоростью 100 км/ч. Найдите среднюю скорость, ответ дайте в км/ч.

8. Первые 100 км поезд прошел со скоростью 50 км/ч, следующие 180 км — со скоростью 70 км/ч, а затем 110 км — со скоростью 110 км/ч. Найдите среднюю скорость, ответ дайте в км/ч.

9. Первый час мотоциклист ехал со скоростью 120 км/ч, следующие три часа — со скоростью 105 км/ч, а затем три часа — со скоростью 65 км/ч. Найдите среднюю скорость.

10. Первые два часа мотоциклист ехал со скоростью 55 км/ч, следующий час — со скоростью 50 км/ч, а затем два часа — со скоростью 40 км/ч. Найдите среднюю скорость.

11. Первые два часа мотоциклист ехал со скоростью 95 км/ч, следующие два часа — со скоростью 75 км/ч, а затем один час — со скоростью 45 км/ч. Найдите среднюю скорость.

[свернуть]

Алгоритм и образцы решения задач на работу

Алгоритм и образцы решения задач на работу

1. После прочтения заполняем схему:

Первый и второй насосы наполняют бассейн за 9 минут, второй и третий — за 14 минут, а первый и третий — за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
- Решение:
- Ответ: 8,4.
Две трубы наполняют бассейн за 3 часа 36 минут, а одна первая труба наполняет бассейн за 6 часов. За сколько часов наполняет бассейн одна вторая труба?
- Решение:
- Ответ: 9.
Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 15 часов. Через 3 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?
- Решение:
- Ответ: 9.
Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 1 минуту дольше, чем вторая труба?
- Решение:
- Ответ: 10.
На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?
- Решение:
- Ответ: 25.

[свернуть]

Тренировочные задания

Тренировочные задания

Задачи на движение по суше

Из двух городов навстречу друг другу одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь от одного города до другого. Второй первую половину пути двигался со скоростью 48 км/ч, а вторую половину пути – со скоростью, на 32 км/ч большей скорости первого, в результате чего прибыл в соседний город в то же время, что первый автомобиль в другой город. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
- Решение:
- Ответ: 64.
Из пункта A в пункт B, расстояние между которыми 12,5 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 50 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 48 минут позже автомобилиста. Ответ дайте в км/ч.
- Решение:
- Ответ: 12,5.
Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
- Решение:
- Ответ: 70.
Автомобиль ехал со скоростью 25 км/ч первые два часа своего пути, следующий час – со скоростью 50 км/ч, а со скоростью 75 км/ч двигался последние два часа. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
- Решение:
- Ответ: 50.
Поезд, двигаясь равномерно со скоростью 40 км/ч, проезжает мимо переезда за 72 секунд. Найдите длину поезда в метрах.
- Решение:
- Ответ: 800.
По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда. Скорость пассажирского поезда 120 км/ч, а товарного — 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 45 секунд. Ответ дайте в метрах.
- Решение:
- Ответ: 525.
Два человека отправляются из одного дома на прогулку до опушки леса, находящейся в 6,6 км от дома. Один идёт со скоростью 5 км/ч, а другой — со скоростью 6 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от дома произойдёт их встреча? Ответ дайте в километрах.
- Решение:
- Ответ: 6.
Между поселками пролегает холмистая местность. Дорога состоит из подъёма и спуска, её полная длина равна 11 км, общее время движения по ней составляет 7 часов. Продолжительность спуска 2 час. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 2 км/ч. Ответ дайте в км/ч.
- Решение:
- Ответ: 3.
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 10 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 20 км/ч больше скорости другого?
- Решение:
- Ответ: 15.
Путешественник переплыл море на яхте со средней скоростью 10 км/ч. Обратно он летел на спортивном самолете со скоростью 240 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
- Решение:
- Ответ: 19,2.

Задачи на движение по течению и против

Моторная лодка прошла против течения реки 56 км и вернулась в пункт отправления, затратив на обратный путь на 3 часа меньше. Найдите скорость течения, если собственная скорость лодки равна 11 км/ч. Ответ дайте в км/ч.
- Решение:
- Ответ: 3.
Моторная лодка в 10:00 вышла из пункта А в пункт В, расположенный в 10 км от А. Пробыв в пункте В 2 часа 10 минут, лодка отправилась назад и вернулась в пункт А в 14:00 того же дня. Определите (в км/ч) собственную скорость лодки, если известно, что скорость течения реки 1 км/ч.
- Решение:
- Ответ: 11.
Весной катер идёт против течения реки в 5/3 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 3/2 раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
- Решение:
- Ответ: 5.

Задачи на движение по течению и против течения

Весной катер идёт против течения реки в 1²⁄3 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1½ раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч). Ответ: 5. (демоверсия, 2013-2021 г.)
Расстояние между пристанями A и B равно 165 км. Из A в B по течению реки отправился плот, а через 1 час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот проплыл 92 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч. Ответ: 16.(досрочная волна, 2021 год)
Теплоход проходит по течению реки до пункта назначения 200 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 15 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 40 часов после отплытия из него. Ответ дайте в км/ч. Ответ: 5.(досрочная волна, Запад; основная волна, Москва, 2020 г.)
Катер в 10:00 вышел из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 1 час, катер отправился назад и вернулся в пункт А в 15:00 того же дня. Определите (в км/час) собственную скорость катера, если известно, что скорость реки равна 2 км/ч. Ответ: 8.(досрочная волна, 2019 г.)
Лодка в 8:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 2 часа, лодка отправилась назад и вернулась в пункт А в 20:00 того же дня. Определите (в км/ч) собственную скорость лодки, если известно, что скорость течения реки равна 2 км/ч. Ответ: 4.(основная волна, 2013 г.)

Задачи на движение вдогонку и навстречу друг другу

Автомобиль, движущийся с постоянной скоростью 70 км/ч по прямому шоссе, обгоняет другой автомобиль, движущийся в ту же сторону с постоянной скоростью 40 км/ч. Каким будет расстояние (в километрах) между этими автомобилями через 15 минут после обгона? Ответ: 7,5.(демоверсия, 2020 г., 2021 г.)

Задачи на движение и на работу

Первая труба наполняет резервуар на 48 минут дольше, чем вторая. Обе трубы, работая одновременно, наполняют этот же резервуар за 45 минут. За сколько минут наполняет этот резервуар одна вторая труба? Ответ: 72.(демоверсия, 2020 г., 2021 г.)
На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий? Ответ: 25.(основная волна, Подмосковье, Санкт-Петербург, 2021 г.)
Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 1 минуту дольше, чем вторая труба? Ответ: 10.(основная волна, Урал, Сибирь, 2021 г.)
Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 77 км. На следующий день он отправился обратно в A со скоростью на 4 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из B в A. Ответ дайте в км/ч. Ответ: 11.(основная волна, Дальний Восток, 2019 г.)
Расстояние между A и B 790 км. Из А в B выехал автомобиль, через 3 часа навстречу ему выехал второй автомобиль со скоростью 75 км/ч. Они встретились на расстоянии 490 км от города А. Найти скорость первого автомобиля. Ответ: 70.(основная волна, Центр, 2019 г.)
Первая труба заполняет бассейн за 7 часов, а две трубы вместе — за 5 часов 50 минут. За сколько часов заполняет бассейн одна вторая труба? Ответ: 35.(досрочная волна, 2016 г.)
Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 19 км. Путь из А в В занял у туриста 13 часов, из которых 6 часов ушёл на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 1 км/ч. Ответ дайте в км/ч. Ответ: 2.(досрочная волна, 2014 г.)
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 128 км. На следующий день он отправился обратно в А со скоростью на 8 км/ч больше прежней. По дороге он сделал остановку на 8 часов. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч. Ответ: 16.(основная волна, 2013 г.)

Задачи на среднюю скорость

Первый час автомобиль ехал со скоростью 115 км/ч, следующие три часа — со скоростью 45 км/ч, а затем два часа — со скоростью 40 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. Ответ: 55.(досрочная волна, 2017 г.)

Задачи на проценты

Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 42 килограммов изюма, если виноград содержит 82% воды, а изюм содержит 19% воды? Ответ: 189.(основная волна, 2013 г.)
Шесть одинаковых рубашек дешевле куртки на 1%. На сколько процентов восемь таких же рубашек дороже куртки? Ответ: 32.(основная волна, 2013 г.)

Задачи на растворы, сплавы

Смешав 45-процентный и 97-процентный растворы кислоты и добавив 10 кг чистой воды, получили 62-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты. Сколько килограммов 45-процентного раствора использовали для получения смеси? Ответ: 15.(демоверсия, 2020 г., 2021 г.)
Имеется два сплава. Первый сплав содержит 40% меди, второй — 25% меди. Масса первого сплава больше массы второго на 10 кг. Из этих двух сплавов получили третий сплав, содержащий 35% меди. Найдите массу третьего сплава. Ответ дайте в килограммах. Ответ: 30.(основная волна, 2016; досрочная волна, 2020 г.)
Имеется два сплава. Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах. Ответ: 36.(досрочная волна, 2013; основная волна, 2016; досрочная волна, 2019 г.)
Имеется два сплава. Первый содержит 15% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 140 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго? Ответ: 70.(досрочная волна, 2019 г.)
Смешав 43‐процентный и 89‐процентный растворы кислоты и добавив 10 кг чистой воды, получили 69‐процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50‐процентного раствора той же кислоты, то получили бы 73‐процентный раствор кислоты. Сколько килограммов 43‐процентного раствора использовали для получения смеси? Ответ: 35.(основная волна, 2014 г.; досрочная волна, 2015 г.)

[свернуть]