ЕГЭ-математика-профиль-задание 4

Задание 4

 — ЕГЭ — профиль-

Вычисление выражений: 

  • базовый уровень сложности; 
  • рекомендуемое время выполнения — 5 минут;
  • за верное решение можно получить 1 балл;
  • решение не проверяется, на апелляцию не подается;
  • все необходимые знания и умения формируются в 7-11 классах

Правил для выполнения этого задания достаточно много, но применяются они практически во всех заданиях «в лоб», то есть никакой сообразительности и супер математической логики не требуется.

Информация для учеников. Как работать с материалом, размещенным в этом разделе?

1.Выучить всю теорию. Не тратьте время на попытки решить наугад. Время дорого!

2. Потренируйтесь в решении дополнительных заданий. Решайте их по алгоритму, отработайте алгоритм так, чтобы выполнять его не задумываясь.

Информация для родителей. Как работать с материалом, размещенным в этом разделе?

Уважаемые неравнодушные и беспокоящиеся родители boast!

Если Вы хотите проконтролировать уровень своего ребенка или помочь ему в изучении методики решения этого задания, то 

  • попросите ученика без каких-либо дополнительных повторений воспроизвести всю теорию. Проверять Вы его можете по тексту на сайте, Вам самим для этого не нужно изучать правила. Воспроизведение должно быть максимально полным и точным.

  • не задавайте наводящих вопросов. Как правило, Ваши вопросы — это скорее подсказки, а они нам не нужны. Пусть ребенок самостоятельно воспроизведет все правила, которые относятся к определенному типу заданий;

  • попросите ученика решить самостоятельно размещенные на сайте образцы. Вы сможете проверить решение по размещенным здесь образцам.

  • просите ребенка, чтобы он объяснял каждый свой шаг, чтобы избежать механического запоминания образца решения. Ведь этот же самый алгоритм нужно будет повторить в задании с другими числами, размещенными в уравнении по другому, а значит нужно запомнить пошаговую логику, а не перемещение символов.

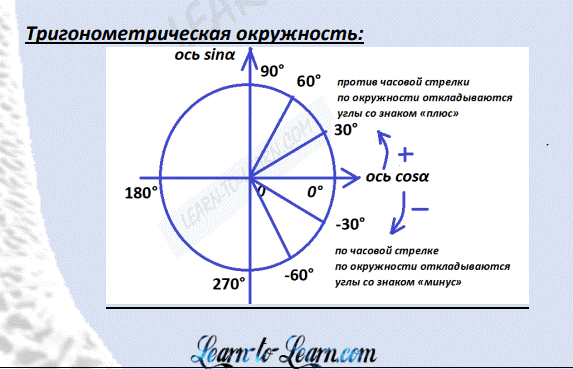
Правила по теме "Тригонометрия"

Правила по теме «Тригонометрия»

  1. синус, косинус, тангенс и котангенс — это тригонометрические функции;
  2. в записи sinα, cosα, tgα, ctgα — α означает  угол альфа;
  3. sinα, cosα, tgα, ctgα  — это математическая запись фраз «синус угла альфа», «косинус угла альфа», тангенс угла альфа», «котангенс угла альфа»;
    • НЕЛЬЗЯ говорить «синус умножить на альфа», «косинус умножить на альфа» и т.д.;
    • НЕЛЬЗЯ разрывать синус и альфа, косинус и альфа;
    • НЕЛЬЗЯ сокращать, умножать складывать и т.д.  функции отдельно от углов, тогда фраза теряет смысл.
  4. углы могут измеряться в градусах (25°; 180°), в радианах (π/3; 2; 5π/4);
  5. углы откладывают по окружности, значения их тригонометрических функций после каждого полного оборота повторяются, поэтому любой угол можно уменьшить или увеличить на 360°, при этом значение функции не изменится;
  6. Основные формулы:

[свернуть]
Образцы решения тригонометрических выражений

Образцы решения тригонометрических выражений

1. Найдите tg a, если cos a = √10/10 , a ∈ (3π/2; 2π).

1. Вспоминаю формулу, связывающую тангенс и косинус: 1+ tg2a=1/cos2a (tga=sina/cosa — не подойдет, так как sina нам не известен):

    \[1+tg^{2}a=\frac{1}{(\frac{\sqrt{10}}{10})^{2}}\]

    \[1+tg^{2}a=\frac{1}{\frac{10}{100}}\]

    \[1+tg^{2}a=\frac{1}{\frac{1}{10}}\]

    \[1+tg^{2}a=10\]

    \[tg^{2}a=9\]

    \[tg a=\pm 3\]

2. По условию угол a находится в четвёртой четверти, то есть тангенс отрицателен.

Ответ: −3.

2. Найдите 5sina, если cosa=2√6/5, a∈( 3π/2; 2π).

1. Вспоминаю формулу, связывающую косинус и синус угла — это основное тригонометрическое тождество: cos2a+sin2a=1.

2. Найдем из основного тригонометрического тождества sina: sin2a = 1-24/25, то есть sin2a=1/25, sinaa=±1/5.

3. Тогда, 5sina=±5•1/5=±1

4. Так как угол находится в 4-ой четверти, то sina=-1.

Ответ: −1.

3. Найдите

    \[\frac{10sin6a}{3cos3a}, sin3a=0,6.\]

1. В числителе вижу формулу синуса двойного угла, поэтому

    \[\frac{10sin6a}{3cos3a}=\frac{10\cdot 2\cdot sin3a\cdot cos3a}{3cos3a}=\frac{20sin3a}{3}\]

2. Подставляем заданное значение:

    \[\frac{20sin3a}{3}=\frac{20\cdot 0,6}{3}=4.\]

Ответ: 4.

4. Найдите значение выражения

    \[\frac{35cos11^{\circ}}{sin79^{\circ}}+7.\]

  

1. Мне нужны одинаковые углы в числителе и знаменателе, поэтому воспользуюсь формулами приведения:

    \[\frac{35cos11^{\circ}}{sin79^{\circ}}+7=\frac{35cos11^{\circ}}{sin(90^{\circ}-11^{\circ})}+7=\frac{35cos11^{\circ}}{cos11^{\circ}}+7=35+7=42\]

Ответ: 42.

5. Найдите значение выражения

    \[\frac{19}{cos^{2}37^{\circ}+1+sin^{2}53^{\circ}}.\]

  

1. Мне нужны одинаковые углы в знаменателе, поэтому воспользуюсь формулами приведения:

    \[\frac{19}{cos^{2}37^{\circ}+1+sin^{2}53^{\circ}}=\frac{19}{cos^{2}(90^{\circ}-53^{\circ})+1+sin^{2}53^{\circ}}=\frac{19}{sin^{2}53^{\circ}+1+sin^{2}53^{\circ}}\]

.

2. В знаменателе вижу основное тригонометрическое тождество:

    \[\frac{19}{sin^{2}53^{\circ}+1+sin^{2}53^{\circ}} =\frac{19}{1+1}=\frac{19}{2}=9,5.\]

.

Ответ: 9,5.

6. Найдите значение выражения

    \[\sqrt{50}cos^{2}\frac{9\pi }{8}-\sqrt{50}sin^{2}\frac{9\pi }{8}.\]

  

1. Вижу общий множитель, выношу его за скобку:

    \[\sqrt{50}cos^{2}\frac{9\pi }{8}-\sqrt{50}sin^{2}\frac{9\pi }{8}=\sqrt{50}(cos^{2}\frac{9\pi }{8}-sin^{2}\frac{9\pi }{8}).\]

.

2. В скобках формула косинуса двойного угла:

    \[\sqrt{50}(cos^{2}\frac{9\pi }{8}-sin^{2}\frac{9\pi }{8})=\sqrt{50}cos(2\cdot \frac{9\pi }{8})=\sqrt{50}cos\frac{9\pi }{4}.\]

.

3. Из значения любого НЕ табличного угла всегда можно вычесть 2π:

    \[\sqrt{50}cos\frac{9\pi }{4}=\sqrt{50}cos (\frac{9\pi }{4}-2\pi )=\sqrt{50}cos\frac{\pi }{4}=\sqrt{50}\cdot \frac{\sqrt{2}}{2}=\frac{\sqrt{100}}{2}=5\]

Ответ: 5.

7. 

8.

9.

10.

11.

[свернуть]
Правила по теме "Логарифмы"

Логарифмические выражения (правила)

  1. logab — логарифм числа b по основанию а; b — подлогарифмическое выражение, а — основание логарифма;
  2. logab, если а=b, то logab=1 (например, log2121=1) (ВСЕГДА!)
  3. logab, если b=1, то logab=0 (например, log321=0) (ВСЕГДА!)
  4. logab=1/logab
  5. logab•Logba=1
  6. при решении логарифмических выражений, уравнений, неравенств нужно стремится к тому, чтобы основания всех логарифмов были одинаковыми и (или) подлогарифмические выражения были одинаковыми;
  7. при решении таких заданий проще работать с обыкновенными дробями;
  8. основные формулы

[свернуть]
Образцы решения логарифмических выражений

Образцы решения логарифмических выражений

1. Найдите значение выражения (log216)•(log636). 

1. Преобразую подлогарифмические выражения так, чтобы они совпадали с основаниями: log224•log662.

2. Преобразую степени подлогарифмических выражений в коэффициенты: log224•log662=4log22•2log66=4•2=8.

Ответ: 8.

2. Найдите значение выражения

    \[7\cdot 5^{log_{5}4}\]

. 

1. Если основание степени совпадает с основанием логарифма, который находится в показатели степени, то

    \[7\cdot 5^{log_{5}4}=7\cdot 4=28\]

.

Ответ: 28.

3. Найдите значение выражения

    \[36^{log_{6}5}\]

. 

1. Чтобы основание степени совпадало с основанием логарифма, который находится в показатели степени, представим 36=62,тогда

    \[36^{log_{6}5}=(6^{log_{6}5})^{2}=(5)^2=25\]

.

Ответ: 25.

4. Найдите значение выражения

    \[log_{0,25}2\]

. 

1. Чтобы основание логарифма совпадало с подлогарифмическим выражением, представим 0,25=1/4=(1/2)2=2-2,тогда

    \[log_{0,25}2=log_{\frac{1}{4}}2=log_{(\frac{1}{2})^2}2=log_{2^{-2}}2=-\frac{1}{2}log_{2}2=-\frac{1}{2}=-0,5\]

.

Ответ: -0,5.

5. Найдите значение выражения log0,310-log0,33. 

1. Разность логарифмов заменяем на логарифм частного: log0,310-log0,33=log0,3(10/3)=log0,3(3/10)-1=-1log0,3(0,3)=-1.

Ответ: -1.

6. Найдите значение выражения

    \[\frac{log_{3}25}{log_{3}5}\]

. 

1. Формулу разности логарифмов здесь применять нельзя.

2. Преобразую подлогарифмическое выражение в числителе так, чтобы оно совпадало с основанием:

    \[\frac{log_{3}25}{log_{3}5}=\frac{log_{3}{5}^2}{log_{3}5}=\frac{2log_{3}5}{log_{3}5}=2.\]

Ответ: 2.

7. Найдите значение выражения

    \[(1-log_{2}12)(1-log_{6}12)\]

. 

1. Как я должен рассуждать? Основания логарифмов и подлогарифмические выражения не совпадают и не могут быть преобразованы так, чтобы полностью совпадать, поэтому применим к каждому логарифму формулу логарифма произведения: 

    \[(1-log_{2}(2\cdot 6))(1-log_{6}(6\cdot 2))=(1-(log_{2}2+log_{2}6))(1-(log_{6}6+log_{6}2))=(1-1-log_26)(1-1-log_{6}2)=-log_{2}6\cdot (-log_6{2})=1\]

. 

Ответ: 1.

8. Найдите значение выражения

    \[(1-log_{2}12)(1-log_{6}12)\]

. 

1. Как я должен рассуждать? Основания логарифмов и подлогарифмические выражения не совпадают и не могут быть преобразованы так, чтобы полностью совпадать, поэтому применим к каждому логарифму формулу логарифма произведения: 

    \[(1-log_{2}(2\cdot 6))(1-log_{6}(6\cdot 2))=(1-(log_{2}2+log_{2}6))(1-(log_{6}6+log_{6}2))=(1-1-log_26)(1-1-log_{6}2)=-log_{2}6\cdot (-log_6{2})=1\]

. 

Ответ: 1.

[свернуть]
Правила по теме "Степени"

Правила по теме «Степени»

 

[свернуть]
Образцы решения выражений со степенями

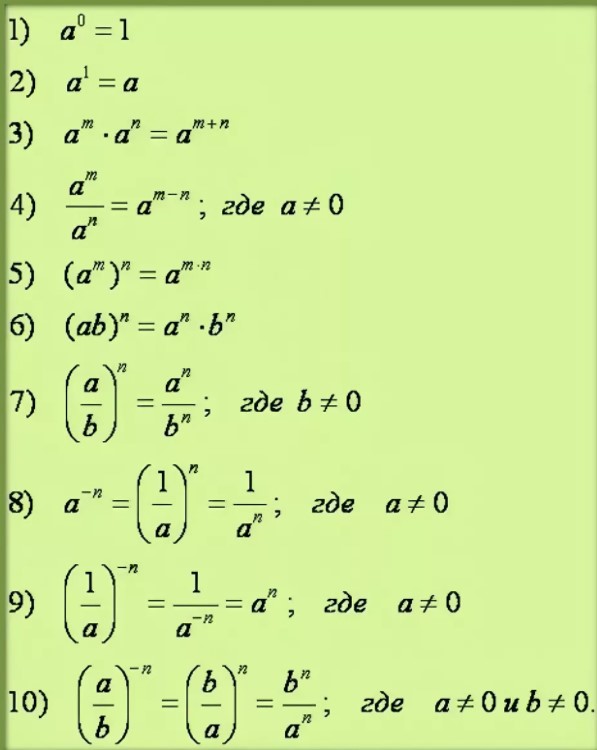
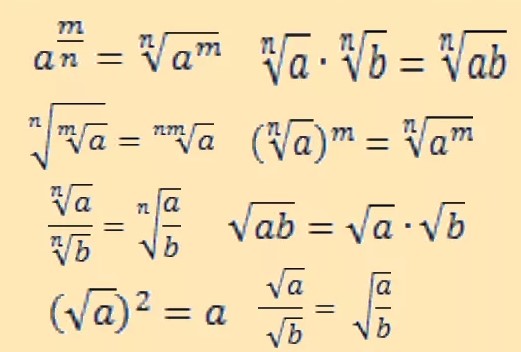
Образцы решения выражений со степенями

1. Найдите значение выражения

    \[\frac{\sqrt[15]{5}\cdot 5\cdot \sqrt[10]{5}}{\sqrt[6]{5}}\]

. 

1. Как я должен рассуждать? Преобразую все корни в степени:

    \[\frac{\sqrt[15]{5}\cdot 5\cdot \sqrt[10]{5}}{\sqrt[6]{5}}=\frac{5^{\frac{1}{15}}\cdot 5^{1}\cdot 5^{\frac{1}{10}}}{5^{\frac{1}{6}}}\]

2. Все основания одинаковые. В числителе все основания перемножаются, поэтому показатели степеней должны складываться: 

    \[\frac{5^{\frac{1}{15}}\cdot 5^{1}\cdot 5^{\frac{1}{10}}}{5^{\frac{1}{6}}}=\frac{5^{\frac{1}{15}+1+\frac{1}{10}}}{5^{\frac{1}{6}}}=\frac{5^{\frac{7}{6}}}{5^{\frac{1}{6}}} \]

.

3. Дробная черта означает деление, поэтому показатели степеней должны вычитаться:

    \[\frac{5^{\frac{7}{6}}}{5^{\frac{1}{6}}}=5^{\frac{7}{6}-\frac{1}{6}}=5^{\frac{6}{6}}=5^{1}=5. \]

 

Ответ: 5.

2. Найдите значение выражения (496)3:(77)5.

Как я должен рассуждать (ВСЕГДА)?

1. При решении заданий со степенями нужны одинаковые основания, поэтому представлю 49 как 72. Тогда, (496)3:(77)5=((72)6)3:(77)5.

2. Чтобы раскрыть скобки со степенями, нужно перемножить показатели, основания оставить без изменения: ((72)6)3:(77)5=736:735.

3. При делении показатели степени вычитаются: 736:735=736-35=71=7.

Ответ: 7.

3. Найдите значение выражения

    \[\frac{\sqrt[5]{10}\cdot \sqrt[5]{16}}{\sqrt[5]{5}}\]

Как я должен рассуждать (ВСЕГДА)?

1. У всех корней одна и та же степень, поэтому могу записать как один корень. Тогда,

    \[\frac{\sqrt[5]{10}\cdot \sqrt[5]{16}}{\sqrt[5]{5}}=\sqrt[5]{\frac{10\cdot 16}{5}}=\sqrt[5]{32}=2.\]

Ответ: 2.

[свернуть]
Правила по теме "Иррациональные выражения"

1. У корней бывают степени. Традиционный корень является квадратным, корнем второй степени, эта степень не указывается, ее просто надо знать.

2. Произведение корней одной и той же степени можно записывать как корень произведения. 

3. Частное корней одной и той же степени можно записать как корень частного.

4. Складывать и вычитать корни одной и той же степени НЕЛЬЗЯ.

5. При раскрытии скобок используется правило «фонтанчика»: каждый множитель перед скобкой должен быть умножен на каждый член в скобках.

[свернуть]
Образцы решения заданий с иррациональными выражениями

Образцы решения заданий с иррациональными выражениями

1. Найдите значение выражения

    \[\sqrt{65^{2}-56^{2}}.\]

Как я должен рассуждать (ВСЕГДА)?

1. Если я вижу формулу сокращенного умножения, то не нужно возводить числа в квадрат, нужно ей воспользоваться,

    \[\sqrt{65^{2}-56^{2}}=\sqrt{(65-56)(65+56)}=\sqrt{9\cdot 121}=3\cdot 11=33.\]

Ответ: 33.

2. Найдите значение выражения

    \[\frac{(2\sqrt{7})^{2}}{14}.\]

Как я должен рассуждать (ВСЕГДА)?

1. Скобки нужно раскрыть, поэтому возведу каждый член в скобках в квадрат:

    \[\frac{(2\sqrt{7})^{2}}{14}=\frac{4\cdot 7}{14}=2.\]

Ответ: 2.

3. Найдите значение выражения

    \[(\sqrt{13}+\sqrt{7})(\sqrt{13}-\sqrt{7}).\]

Как я должен рассуждать (ВСЕГДА)?

1. Если я вижу формулу сокращенного умножения, я обязан ее применить:

    \[(\sqrt{13}+\sqrt{7})(\sqrt{13}-\sqrt{7})=(\sqrt{13})^{2}-(\sqrt{7})^{2}=13-7=6.\]

Ответ: 6.

4. Найдите значение выражения

    \[(\sqrt{3\frac{6}{7}}-\sqrt{1\frac{5}{7}}):\sqrt{\frac{3}{28}}. \]

Как я должен рассуждать (ВСЕГДА)?

1. Скобки нужно раскрыть, использую правило «фонтанчик»:

    \[(\sqrt{3\frac{6}{7}}-\sqrt{1\frac{5}{7}}):\sqrt{\frac{3}{28}}=\sqrt{3\frac{6}{7}:\frac{3}{28}}-\sqrt{1\frac{5}{7}:\frac{3}{28}}\]

2. Теперь выполняю деление дробей:

    \[\sqrt{3\frac{6}{7}:\frac{3}{28}}-\sqrt{1\frac{5}{7}:\frac{3}{28}}=\sqrt{\frac{27}{7}\cdot \frac{28}{3}}-\sqrt{\frac{12}{7}\cdot \frac{28}{3}}=\sqrt{36}-\sqrt{16}=6-4=2. \]

Ответ: 2.

5. Найдите значение выражения

    \[\frac{(\sqrt{13}+\sqrt{7})^{2}}{10+\sqrt{91}}.\]

Как я должен рассуждать (ВСЕГДА)?

1. Вижу формулу сокращенного умножения, значит, использую ее:

    \[\frac{(\sqrt{13}+\sqrt{7})^{2}}{10+\sqrt{91}}=\frac{13+2\sqrt{91}+7}{10+\sqrt{91}}=\frac{20+2\sqrt{91}}{10+\sqrt{91}}\]

2. Вижу, что в числителе могу вынести общий множитель за скобку:

    \[\frac{20+2\sqrt{91}}{10+\sqrt{91}}=\frac{2(10+\sqrt{91})}{10+\sqrt{91}}=2 \]

Ответ: 2.

[свернуть]
Алгоритм и образец решения выражений с подстановкой

Выражения с подстановкой

1. Найдите значение выражения 5(4р(х+2) — р (4х)), при р (х) = х-2.

1.р(х) — это функция р от переменной х.

2. По условию р(х)=х-2. Мне нужно найти р(х+2), для этого в выражение для р(х) вместо х подставляю (х+2), получаю

р(х+2)=(х+2)-2=х+2-2=х.

3. По условию р(х)=х-2. Мне нужно найти р(4х), для это в выражение для р(х) вместо х подставлю (4х), получаю

р(4х)=(4х)-2=4х-2.

4. Подставляю все найденные значения в заданное выражение

5(4р(х+2) — р (4х))=5•(4•х-(4х-2))=5•(4х-4х+2)=5•2=10.

Ответ: 10.

[свернуть]
Тренировочные задания

Тренировочные задания

Тригонометрические выражения

  1. Найдите  синус 2\alpha, если  косинус \alpha = 0,6 и  Пи меньше \alpha меньше 2 Пи . Ответ: -0,96. (Демонстрационная версия-2021)
  2. Найдите значение выражения  дробь, числитель — 5 синус 98 в степени \circ , знаменатель — синус 49 в степени \circ умножить на синус 41 в степени { \circ }. Ответ: 10. (Основная волна-2021)
  3. Найдите значение выражения  дробь, числитель — 24({{ синус } в степени 2 }17{} в степени circ минус {{ косинус } в степени 2 }17{} в степени circ ), знаменатель — косинус 34{ в степени circ }. Ответ: -24. (Основная волна-2021)
  4. Найдите значение выражения 2 корень из 2 косинус в степени 2 { дробь, числитель — 3 Пи , знаменатель — 8 } минус корень из 2 . Ответ: -1. (Досрочная волна-2019)
  5. Найдите значение выражения 5 синус дробь, числитель — 11 Пи , знаменатель — 12 умножить на косинус дробь, числитель — 11 Пи , знаменатель — 12 . Ответ: -1,25. (Основная волна-2014)
  6. Найдите 4 косинус 2\alpha, если  синус \alpha = минус 0,5. Ответ: 2. (Досрочная волна. 2013)
  7. Найдите значение выражения  минус 50 тангенс 9 в степени circ умножить на тангенс 81 в степени circ плюс 31.  Ответ: -19. (Основная волна-2013)
  8. Найдите значения выражения  дробь, числитель — 23, знаменатель — синус в степени 2 56 в степени circ плюс 1 плюс синус в степени 2 146 в степени circ . Ответ: 11,5 . (Основная волна-2013)
  9. Найдите значение выражения  дробь, числитель — 7 косинус 80 в степени \circ , знаменатель — синус 10 в степени \circ минус 3.  Ответ: 4. (Досрочная волна-2013)

Выражения со степенями

  1. Найдите значение выражения: 4 в степени д робь, числитель — 1, знаменатель — 5 умножить на 16 в степени д робь, числитель — 9, знаменатель — 10 . Ответ: 16. (Демонстрационная версия-2021)
  2. Найдите значение выражения  дробь, числитель — (5 корень из { 6}) в степени 2 , знаменатель — 10 . Ответ:15. (Досрочная волна -2020)
  3. Найдите значение выражения  дробь, числитель — левая круглая скобка 5 в степени дробь, числитель — 3, знаменатель — 5 , знаменатель — cdot7 в степени { дробь, числитель — 2, знаменатель — 3 правая круглая скобка в степени 15 }{35 в степени 9 }. Ответ: 7. (Досрочная волна-2016)
  4. Найдите значение выражения 0,75 в степени дробь, числитель — 1, знаменатель — 8 умножить на 4 в степени дробь, числитель — 1, знаменатель — 4 умножить на 12 в степени дробь, числитель — 7, знаменатель — 8 . Ответ: 12. (Досрочная волна-2016)
  5. Вычислите:  дробь, числитель — корень из [ 28]3 умножить на 3 умножить на корень из [ 21]3, знаменатель — корень из [ 12]3 . Ответ: 3. (Досрочная волна-2015)

Выражения с логарифмами

  1. Найдите значение выражения: 16 логарифм по основанию 7 корень из [ 4]{7}. Ответ: 4. (Демонстрационная версия-2021)
  2. Найдите значение выражения  дробь, числитель — логарифм по основанию 2 49, знаменатель — логарифм по основанию 2 7 . Ответ: 2. (Основная волна-2019)
  3. Найдите значение выражения  логарифм по основанию 0,25 128 минус логарифм по основанию 0,25 2. Ответ: -3. ( Основная волна-2019)
  4. Найдите значение выражения  логарифм по основанию 5 7 умножить на логарифм по основанию 7 25. Ответ: 2. (Досрочная волна-2014)

Выражения с корнями

  1. Найдите значение выражения  корень из { {{89} в степени 2 } минус {{39} в степени 2 }}. Ответ: 80. (Досрочная волна-2019)
  2. Найдите значение выражения  дробь, числитель — корень из [ 3]{121} умножить на корень из [ 4]{121}, знаменатель — корень из [ 12]{121 }. Ответ: 11. (Досрочная волна-2017)
  3. Найдите значение выражения ( корень из { 63} −  корень из { 28})  умножить на корень из { 7}.  Ответ: 7. (Основная волна-2013)

[свернуть]

©  2024 Learn-to-learn.com. Создано с помощью WordPress и темы Highlight Theme