Задания 11
— ЕГЭ — профиль-
— вероятность и комбинаторика-
- базовый уровень сложности;
- рекомендуемое время выполнения — 5 минут /достаточно 2-х минут/;
- за верное решение можно получить 1 балл;
- решение не проверяется, на апелляцию не подается;
- все необходимые знания и умения формируются в 5-9 классах;
Задание совсем не трудное, но многие в школах пропустили эту тему, посчитав ее не серьезной, а в 10-11 классах повторения этого материала нет. Но ничего страшного, правил здесь не много, Вы быстро все восстановите.
Информация для учеников. Как работать с материалом, размещенным в этом разделе?
1шаг. Обязательно выучить алгоритм.
2 шаг. При решении проговаривать каждый шаг алгоритма полностью, не ленится, не заменять формулировки алгоритма на другие фразы (даже, если Вам кажется, что у них тот же смысл).
3 шаг. Если произносить не получается, то записывайте каждый шаг алгоритма.
4 шаг. Выполняя шаги алгоритма, отвечайте именно на те вопросы, что Вам задаются, не придумывайте свои.
Информация для родителей. Как работать с материалом, размещенным в этом разделе?
Уважаемые неравнодушные и беспокоящиеся родители  !
!
Если Вы хотите проконтролировать уровень своего ребенка или помочь ему в изучении методики решения этого задания, то
-
попросите ученика без каких-либо дополнительных повторений воспроизвести всю теорию. Проверять Вы его можете по тексту на сайте, Вам самим для этого не нужно изучать правила. Воспроизведение должно быть максимально полным и точным.
-
не задавайте наводящих вопросов. Как правило, Ваши вопросы — это скорее подсказки, а они нам не нужны. Пусть ребенок самостоятельно воспроизведет все правила, которые относятся к определенному типу заданий;
-
попросите ученика решить самостоятельно размещенные на сайте образцы. Вы сможете проверить решение по размещенным здесь образцам. Просите ребенка, чтобы он объяснял каждый свой шаг, чтобы избежать механического запоминания образца решения. Ведь этот же самый алгоритм нужно будет повторить в задании с другими числами, размещенными в уравнении по другому, а значит нужно запомнить пошаговую логику, а не перемещение символов.
Дополнение:
Можно ли учить не всю теорию? Нельзя.
Чем больше заданий Вы выполните, тем быстрее правила закрепятся в памяти, поэтому практика, практика и еще раз практика.
Можно ли решать другим способом? Да, конечно. Если Ваш способ никогда Вас не подводит, то ни в коем случае от него не отказывайтесь, не переучивайтесь, у Вас и так все будет хорошо.
Основные типы заданий
- Вероятность сесть, войти, пойти, участвовать вместе с кем-то, рядом с кем-то или, напротив, не рядом, не вместе и т.д.
- Вероятность получить (выбрать) именно данный предмет.
- Вероятность попасть в цель.
- Найти вероятность победы или проигрыша команды.
- Найти вероятность в некоторых пределах.
- Найти вероятность события в определенный день.
- Вероятность в задачах о кубиках (игральных костях).
- Вероятность выбора определенной дорожки.
- Вероятность приобрести качественный/некачественный товар.
- Вероятность того, что товар пойдет в переработку.
Учим!
- Вероятность = хочу/всего. Хочу — это не одна ситуация, а все ситуации, которые соответствуют нашим желаниям.
- Если какое-то место уже занято, то общее количество мест нужно уменьшить на одно. Если занято большее количество мест, то на столько же нужно уменьшить общее количество.
- Если одно из мест занято соотечественником, то количество «хочу» нужно уменьшить на количество соотечественников.
- Если нам подходят все перечисленные вероятности и не важно какая из них сбудется, то все вероятности мы складываем.
- Если нам нужно, чтобы все вероятности сбылись или произошли одновременно, или вероятности зависят друг от друга, то мы эти вероятности перемножаем.
- Если в задаче много неизвестных, вводим переменные. Их можно вводить сколько угодно, но, чем меньше, тем лучше.
- Если нужно найти вероятность, что несколько человек (предметов) окажутся в одной группе (в одинаковых условиях), нужно предположить, что один из людей (предметов) уже в этой группе, найти вероятность этого обычным способом. Затем найти вероятность того, что второй человек тоже попал в эту группу, не забыть уменьшить количество желаемых и общих мест на один. Затем найти вероятность того, что третий человек попадет в эту группу, обязательно уменьшить количество желаем и общих мест еще на один. И т.д. Все найденные вероятности нужно перемножить.
- Для нахождения вероятности выигрыша (проигрыша) команды нужно составить таблицу всех возможных событий. Не ленитесь, таблица может казаться большой, но тогда Вы не потеряете и не приобретете лишние данные. Выделите в этой таблице желаемые результаты, поделите это значение на общее количество ситуаций в таблице. В таблице можно просто указывать плюсы и минусы, а можно вписывать баллы, если они заданы в условии задачи.
1 команда 2 команда 3 команда 1 вариант + + + 2 вариант + + — 3 вариант + — — и т.д. - Если нужно найти вероятность в каких-то пределах, то можно построить координатный луч, отметить на нем все данные величины, дугами показать все вероятности. Дальнейшие шаги зависят от того, нужно найти часть чего-то (тогда нужно вычитать) или совокупность каких-то вероятностей (тогда нужно складывать).
- Общая вероятность равна 1. Больше не бывает. Вероятность может быть равна 0, то есть это событие никогда не произойдет.
- Если нужно найти вероятность события в определенный день, находим количество мест в этот день, делим на общее количество мест. Чтобы найти количество мест в определенный день, нужно из общего количества мест вычесть количество мест в другие (не интересующие нас дни). «В первые 2 дня по 5 докладов» = и в первый день 5 докладов, и во второй день 5 докладов, то есть всего за первые два дня всего 10 докладов (мест)! «Распределены поровну на 3 дня» = какое-то количество надо поделить на 3.
- Если нужно найти вероятность в задаче о кубиках, то чертим полную таблицу 6 на 6, не ленимся!!! Обводим в кружок желаемые результаты, делим это число на общее количество событий.

- Если вероятности отдельных событий уже дана, то еще раз искать ее не надо!!! Нужно понять зависят ли они друг от друга (нужно перемножить); не зависят ли они друг от друга и нам подходят все (надо складывать); или они являются частями полной вероятности (единицы), а нам нужно найти недостающую часть (нужно их сложить и результат вычесть из 1).
- Округление числа:
- подчеркнуть позицию, до которой надо округлить;
- если цифра, стоящая правее, менее 5 (0,1,2,3,4), то отбрасываем ее и все, что стоит еще правее, получаем ответ;
- если цифра, стоящая правее, равна 5,6,7,8 или 9, то подчеркнутую цифру увеличиваем на один, все, что стоит правее отбраасываем, получим ответ.
- Если задача большая, много текста, начните с вопроса. Что от меня хотят? Как я это умею искать? Записываю формулу. Каких данных мне не хватает, чтобы дать ответ? Ищу недостающие данные.
- Трудная формула, но некоторые задачи позволяет решить быстрее, чем обычные рассуждения.
![Rendered by QuickLaTeX.com \[P=C_{n}^{k}\cdot p^{k}\cdot q^{n-k}, C_{n}^{k}=\frac{n!}{k!(n-k)!}\]](https://learn-to-learn.com/wp-content/ql-cache/quicklatex.com-d60b2d1c534494012cc4d0a3d1fe4e1e_l3.png)
- С — вероятность;
- n-количество всех ситуаций;
- k — количество желаемых ситуаций;
- p- вероятность желаемых ситуаций;
- q — вероятность нежелательных ситуаций (1-р).
- ! — знак факториала, означает, что нужно перемножить все числа от 1 до того числа, которое указано под знаком факториала. например, 5!=1·2·3·4·5=120.
- Сначала находим С, подставляем найденное значение в первую формулу.
17. Если дана вероятность того, что событие свершиться, а нужна вероятность противоположного события, то нужно из единицы вычесть заданную вероятность.
18. Если в задаче много ситуаций, спокойно рассматриваем все поочередно, не нервничаем!
Алгоритм решения
1.Чего хочу по условию задачи? (отвечаем 1-2 словами, не более)
2.Сколько возможностей, ситуаций, которые я хочу? Записываю: хочу — … (число).
3. Сколько всего ситуаций, возможностей? Записываю: всего — … (число).
4. Подставляю найденные числа в формулу, вычисляю.
Образцы решений
Если Вы сами не смогли решить задачу, то ВЫУЧИТЕ представленное решение, а не просто просмотрите или спишите его.
Задание 1.
За круглый стол на 11 стульев в случайном порядке рассаживаются 9 мальчиков и 2 девочки. Найдите вероятность, что девочки окажутся на соседних местах.
Решение:
1. вероятность=хочу/всего.
2. Предположим, что одна из девочек уже села на какой-то стул. Вторая девочка хочет сеть рядом, таких подходящих стульев только 2 (хочу).
3. Так как одна из девочек уже села, один стул занят, свободных для второй девочки осталось 10 (всего).
4. Вероятность = 2/10=0,2.
Задание 2.
Какова вероятность того, что последние две цифры телефонного номера в сумме дают 10.
Решение:
1. вероятность=хочу/всего.
2. Перечислим все ситуации, когда сумма последних двух цифр даст 10: 1+9;9+1;2+8;8+2;3+7;7+3;4+6;6+4;5+5. Таких ситуаций 9 (хочу).
3. Все возможные наборы последних цифр: от 00 до 99, то есть 100 штук (всего).
4. Вероятность = 9/100=0,09.
Задание 3.
В среднем из 3000 садовых насосов, поступивших в продажу, 12 подтекают. Найдите вероятность того, что один случайно выбранный насос не подтекает.
Решение:
1. вероятность=хочу/всего.
2. Найдем вероятность того, что насос подтекает (формула та же): 12/3000=0,004.
3. Чтобы найти противоположную вероятность (то, что насос не подтекает), нужно из 1-0,004=0,996.
Задание 4
Стрелок в тире стреляет по мишени до тех пор, пока не попадет в нее. Вероятность попадания при каждом отдельном выстреле равна р=0,6. Найдите вероятность того, что стрелку потребуется ровно три попытки.
Решение:
1.Чего хочу? Чтобы стрелок попал с третьей попытки.
2. Для этого он должен первые два раза обязательно промахнуться. То есть нужно такое сочетание событий: промах, промах, в цель. Эти события обязательно должны произойти все, поэтому их вероятности нужно перемножить.
3. Вероятность промаха: 1-0,6=0,4
4. 0,4•0,4•0,6=0,096.
Задание 5.
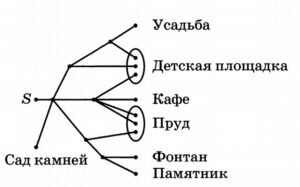
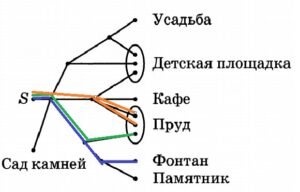
Артем гуляет по парку. Он выходит из точки S и, дойдя до очередной развилки, с равными шансами выбирает следующую дорожку, но не возвращается обратно. Найдите вероятность того, что он выйдет к пруду или фонтану.
Решение:
1. Определим подходящие ситуации. У каждой ситуации свой цвет. Всего 3 ситуации.
2. Найдем вероятность каждой ситуации, для этого рассмотрим каждый узел в отдельности. Синяя вероятность: 1/4•1/2•1/2=1/16. Зеленая вероятность: 1/4•1/2=1/8. Оранжевая вероятность: 1/4•2/4=1/8.
3. Нас устроит любая из этих ситуаций, поэтому мы складываем их вероятности (они не обязательно должны произойти все, они не зависят друг от друга).1/16+1/8+1/8=5/16=0,3125.
Задание 6.
На конференцию приехали ученые из трех стран 7 из Сербии, 3 из России и 2 из Дании. Каждый из них делает на конференции один доклад. Найдите вероятность того, что десятым окажется доклад ученого из России.
1. Вероятность=хочу/всего.
2. Чтобы десятым оказался кто-то из России есть 3 возможности (хочу).
2. Всего десятым могут выступить 7+3+2=12 человек.
3. Вероятность=3/12=0,25.
Задание 7.
В группе туристов 20 человек. Их вертолетом доставляют вертолетом, перевозя по 4 человека за рейс. Найдите вероятность того, что турист В. полетит первым рейсом.
Решение:
1. Вероятность=хочу/всего.
2. Чтобы полететь первым рейсом есть 3 возможности (хочу).
2. Всего разных вариантов полететь 20 мест.
3. Вероятность=3/20=0,2.
Задание 8.
На уроке физкультуры 26 школьников, из них 12 девочек, остальные — мальчики. По сигналу учителя все строятся в шеренгу. Найдите вероятность, что первые двое окажутся мальчиками.
Решение:
1. Вероятность=хочу/всего.
2. Количество мальчиков: 26-12=14.
3. Вероятность того, что первым будет мальчик: 14/26.
4. Вероятность того, что вторым будет мальчик (с учетом, что первый уже мальчик): 13/25.
5. Эти вероятности обязательно должны реализоваться обе, поэтому мы их перемножаем: 14/26 • 13/25 =0,28.
Задание 9.
По отзывам покупателей Петр Петрович оценил надежность двух интернет-магазинов. Вероятность того, что товар доставят из одного магазина, равна 0,8, а вероятность доставки из другого равна 0,95. Петр Петрович заказ товар в обоих магазинах. Найдите вероятность, что оба магазина доставят товар.
Решение:
1. Так как необходимо, чтобы оба магазина доставили товар, вероятности перемножаем: 0,8•0,95=0,76
Задание 10.
Из ящика, в котором лежат фломастеры, не глядя достали два фломастера. Найдите вероятность того, что эти фломастеры оказались одного цвета, если известно, что в ящике 12 синих и 13 красных фломастеров.
Решение:
1. Вероятность=хочу/всего.
2. Нам подойдут две ситуации: достанут два синих или два красных фломастера.
3. Вероятность того, что первым достанут синий 12/25, вероятность того, что вторым достанут тоже синий 11/24. Эти вероятности должны совпасть, поэтому мы их перемножаем: 12/25 •11/24=11/50.
4. Вероятность того, что первым достанут красный 13/25, вероятность того, что вторым достанут тоже красный 12/24. Эти вероятности должны реализоваться обязательно обе, поэтому мы их перемножаем: 13/25 • 12/24=13/50.
5. Нам не важно какая именно ситуация реализуется, поэтому вероятности каждой из них просто складываем: 11/50+13/50=24/50=0,48.
Задание 11.
В чемпионате участвуют 51 спортсмен, среди которых 14 спортсменов из России, в том числе, спортсмен Т. Найдите вероятность того, что в первом туре он будет играть с каким-либо спортсменом из России.
Решение:
1. Вероятность=хочу/всего.
2. Так как спортсмен Т. сам из России, то желаемых соперников у него 13, а всего он сможет сыграть с 50 спортсменами.
3. Вероятность= 13/50=0,26
Задание 12.
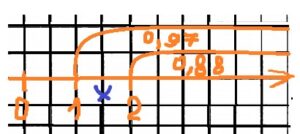
Вероятность того, что фен прослужит больше 1 года, равна 0,97. Вероятность того, что он прослужит больше 2 лет, равна 0,88. Найдите вероятность того, что он прослужит больше одного, но меньше двух лет.
Решение:
1. Для решения таких задач полезно построить координатный луч и отметить на нем все данные.
2. Вероятность отрезка между 1 и 2 годами: 0,97-0,88=0,09
Задание 13.
В коробке 8 черных шаров и 5 белых. Достают 6 шаров. Во сколько раз событие «среди выбранных шаров ровно 4 черных» более вероятно, чем событие «среди выбранных шаров ровно 5 черных»?
Решение:
1. Ситуация первая: из 6 шаров достают 4 черных (то есть 2 белых). Это можно сделать 6!:(4!•2!) способами.
2. Ситуация вторая: из 6 шаров достают 5 черных (то есть один белый). Это можно сделать 6!:(5!•1!) способами.
3. Чтобы найти во сколько отличается первая ситуация от второй, нужно их поделить:
Задание 14.
Два автомобилиста, независимо друг от друга, выезжают из пункта А в пункт В. Навигатор предлагает каждому из них 8 равноценных маршрутов, и автомобилисты выбирают маршрут случайным образом. Найдите вероятность того, что автомобилисты выберут различные маршруты.
Решение:
1. Вероятность=хочу/всего.
2. Для второго автомобилиста желаемых маршрутов всего 7, так как один из маршрутов выберет первый. Всего маршрутов по условию 8.
3. вероятность=7/8=0,875
Задание 16.
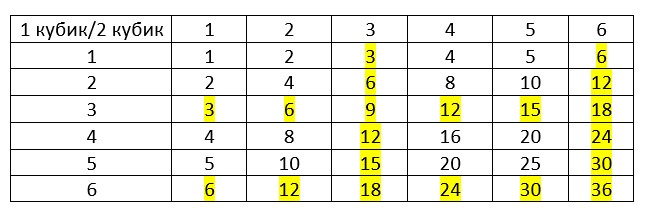
Игральную кость бросают дважды. Найдите вероятность того, что произведение выпавших очков делится на 3. Ответ округлите до тысячных.
Решение:
1. Вероятность=хочу/всего.
2. Составим таблицу бросков, выделим в ней подходящие:
3. Всего вариантов: 36; подходящих: 20.
4. Вероятность=20/36≈0,556.
Задание 17.
Игральную кость бросают дважды. Известно, что сумма выпавших очков больше 8. Найдите вероятность события «при втором броске выпало 6 очков».
Решение:
1. Вероятность=хочу/всего.
2. В этом задании можно составить таблицу бросков и выделить в ней подходящие, а можно просто выписать все возможные ситуации, так как их не много: 3+6; 6+3; 4+5; 5+4; 4+6; 6+4; 5+5; 5+6; 6+5; 6+6. Всего: 10, из них при втором броске выпадает 6 в 4 случаях.
3. Вероятность=4/10=0,4
Задание 18.
Всего в группе туристов 51 человек, в том числе Иван и Егор. Группу случайным образом делят на три подгруппы по 17 человек для посадки в три автобуса. Известно, что Иван оказался в третьем автобусе. Какова вероятность того, что при этом условии Егор окажется в первом автобусе?
Решение:
1. Вероятность=хочу/всего.
2. Подходящих мест для Егора в первом автобусе: 17, всего для него мест во всех автобусах (с учетом, что в третьем сидит Иван): 50.
3. Вероятность=17/50=0,34
Задание 19.
В магазине в одной коробке лежат вперемешку ручки с чёрными, синими или красными чернилами одинаковые на вид. Покупатель случайным образом выбирает одну ручку. Вероятность того, что она окажется чёрной, равна 0,37, а того, что она окажется синей, равна 0,45. Найдите вероятность того, что ручка окажется красной.
Решение:
1. Полная вероятность=1.
2. Вероятность красной ручки=1-0,37-0,45=0,18.
Задание 20.
В кафе на одной полке в случайном порядке стоят 50 чайных чашек: 30 зелёных, 10 красных и 10 синих. На другой полке в случайном порядке стоят 50 блюдец: 30 зелёных, 10 красных и 10 синих. Найдите вероятность того, что случайно выбранные чашка и блюдце будут одинакового цвета.
Решение:
1. Нас устроят ситуации: чашка и блюдце красные, чашка и блюдце синие, чашка и блюдце зеленые. Так как эти ситуации не зависят друг от друга, то их вероятности нужно сложить.
2. Вероятность красных чашки и блюдца: 10/50 •10/50=1/25.
3. Вероятность синих чашки и блюдца: 10/50 •10/50=1/25.
4. Вероятность зеленых чашки и блюдца: 30/50 •30/50=9/25.
5. Вероятность одинакового цвета=1/25+1/25+9/25=11/25=0,44
Задание 21.
Научная конференция проводится в 4 дня. Всего запланировано 50 докладов: первые два дня — по 13 докладов, остальные распределены поровну между третьим и четвёртым днями. На конференции планируется доклад профессора К. Порядок докладов определяется случайным образом. Какова вероятность того, что доклад профессора К. окажется запланированным на последний день конференции?
Решение:
1. Вероятность=хочу/всего.
2. В последний день конференции вакантных мест: (50-13-13):2=12 человек. Всего мест: 50.
3. Вероятность: 12/50=0,24.
Задание 22.
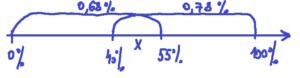
Гигрометр измеряет влажность в помещении картинной галереи. Вероятность того, что влажность окажется выше 40%, равна 0,78. Вероятность того, что влажность окажется ниже 55 %, равна 0,68. Найдите вероятность того, что влажность находится в пределах от 40 % до 55 %.
Решение:
1. Начертим координатный луч и отметим на нем все заданные условия:
2. Найдем вероятность, что влажность от 0% до 40%: 1-0,78=0,22.
3. Найдем влажность от 40% до 55%: 0,68-0,22=0,46.
Задание 23.
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
Решение:
1. Хочу, чтобы команда вышла.
2. Чтобы команда вышла, нужно набрать 4 и более очков из двух игр
- нужно два раза выиграть,
- нужно первый раз выиграть/второй сыграть в ничью,
- нужно первый раз сыграть в ничью/второй выиграть.
- нас устроит любой из этих вариантов, поэтому их вероятности складываем.
3. Вероятность выигрыша 0,4, проигрыша 0,4, ничьей 0,2.
4. Вероятность = 0,4•0,4+0,4•0,2+0,2•0,4=0,32.
Задание 24.
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Финиш» играет три матча с разными командами. Найдите вероятность того, что в этих матчах команда «Финиш» начнёт игру с мячом ровно два раза.
Решение:
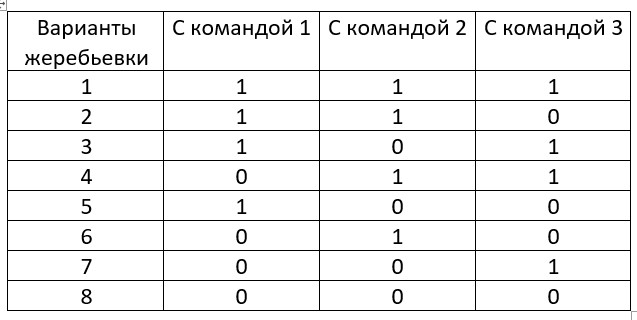
1. Составим таблицу жеребьевки:
2. Нам подходят варианты 2,3,4, то есть 3 штуки, всего 8 вариантов.
2. Вероятность = 3/8=0,375.
Тренировочные задания
Задачи на расчет вероятности с помощью формулы: хочу/всего
- В сборнике билетов по биологии всего 30 билетов. Только в шести билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.
- В сборнике билетов по математике всего 28 билетов, в 14 из них встречается вопрос по теме «Неравенства». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по теме «Неравенства».
- В фирме такси в наличии 51 легковых автомобилей; 27 из них чёрного цвета с жёлтыми надписями на бортах, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
- В соревнованиях по лёгкой атлетике участвуют 11 спортсменов из Финляндии, 5 спортсменов из Дании, 10 спортсменов из Словении и 4 — из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Словении.
- В среднем из 2000 садовых насосов, поступивших в продажу, 14 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает?
- Фабрика выпускает сумки. В среднем 13 сумок из 200 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов.
- Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Труд» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Труд» выиграет жребий ровно два раз?
- Перед началом волейбольного матча капитаны команд тянут жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Мотор» по очереди играет с командами «Статор», «Стартер» и «Ротор». Найдите вероятность того, что «Мотор» будет начинать с мячом только первую игру.
- Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Сапфир» играет три матча с разными командами. Найдите вероятность того, что в этих матчах команда «Сапфир» начнёт игру с мячом более двух раза.
- В группе туристов 10 человек. С помощью жребия они выбирают семерых человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Г., входящий в состав группы, пойдёт в магазин?
- Конкурс исполнителей проводится в 5 дней. Всего заявлено 110 выступлений — по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 10 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление исполнителя из России состоится в третий день конкурса?
- Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 6, но не дойдя до отметки 9.
- Первый игральный кубик обычный, а на гранях второго кубика нет нечетных чисел, а четные числа 5,6 встречаются по три раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 5 и 6. Какова вероятность, что бросали первый кубик?
Задачи на использование формулы суммы вероятностей несовместных событий
- На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,27. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,33. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
- Вероятность того, что мотор холодильника прослужит более 1 года, равна 0,7, а вероятность того, что он прослужит более 2 лет, равна 0,42. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?
- Вероятность того, что новый сканер прослужит больше года, равна 0,92. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Задачи на расчет вероятности с помощью формулы: хочу/всего
- В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах. Ответ: 0,08. (Демонстрационная версия. 2021)
- В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по теме «Неравенства». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по теме «Неравенства». Ответ: 0,6. (Основная волна. 2019 и 2021)
- В фирме такси в наличии 45 легковых автомобилей; 18 из них чёрного цвета с жёлтыми надписями на бортах, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями. Ответ: 0,6. (Досрочная волна. 2019)
- В соревнованиях по лёгкой атлетике участвуют 6 спортсменов из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Словении и 8 — из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Словении. Ответ: 0,3. (Досрочная волна. 2019)
- В среднем из 2000 садовых насосов, поступивших в продажу, 6 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает? Ответ: 0,997. (Основная волна. 2014)
- Фабрика выпускает сумки. В среднем 8 сумок из 100 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов. Ответ: 0,92. (Основная волна. 2021)
- Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Труд» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Труд» выиграет жребий ровно один раз? Ответ: 0,375. (Досрочная волна. 2019)
- Перед началом волейбольного матча капитаны команд тянут жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Мотор» по очереди играет с командами «Статор», «Стартер» и «Ротор». Найдите вероятность того, что «Мотор» будет начинать с мячом только вторую игру. Ответ: 0,125. (Досрочная волна. 2019)
- Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Сапфир» играет три матча с разными командами. Найдите вероятность того, что в этих матчах команда «Сапфир» начнёт игру с мячом не более одного раза. Ответ: 0,5. (Досрочная волна. 2017)
- В группе туристов 8 человек. С помощью жребия они выбирают шестерых человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Г., входящий в состав группы, пойдёт в магазин? Ответ: 0,75. (Резервная волна. 2021)
- Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений — по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление исполнителя из России состоится в третий день конкурса? Ответ: 0,225. (Досрочная волна. 2018)
- Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 12, но не дойдя до отметки 3. Ответ: 0,25. (Досрочная волна. 2021)