Составить уравнение
| фигура | вид | дано | формула | подробнее |
| вектор ē | в виде координат | А(хА; уА); В(хВ; уВ) | ē (хВ-хА; уВ-уА) | |
| вектор ē | в виде координат | ā (хА; уВ);
ū (хu; yu); ē=L•ā±S•ū |
ē(L•хА ± S•xВ ; L•yА ± S•yВ ) | |
| вектор ē | в виде координат | |ē|=S
ā=m•i+n•j+k•z ā||ē |
1. у параллельных (коллинеарных) векторов соответствующие коэффициенты пропорциональны, записываем координаты искомого вектора с помощью коэффициента пропорциональности
2. подставляем координаты искомого вектора в теорему Пифагора, с помощью известной длины искомого вектора, находим коэффициент пропорциональности 3. домножаем координаты заданного вектора на коэффициент пропорциональности, получаем координаты искомого вектора. если искомый вектор направлен противоположно, то у его координат ставим противоположные знаки |
|
| вектора | в виде координат (или разложения по i,j,k), заданы векторы, перпендикулярные искомому |
|
||
| прямой | с угловым коэффициентом | у=кx+b; к=(y2-y1)/(x2 -x1) | ||
| прямой | в виде двух пересекающихся плоскостей | направляющий вектор находится с помощью матрицы i, j, k и коэффициентов из системы. |
||
| прямой | проходящей через две точки | |||
| прямой | проходящая через точку (х0, y0, z0) и имеющей направляющий вектор a(m,n,p) (канонический вид) | |||
| прямой | параметрическое уравнение | 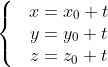
получается из канонического, если каждую дробь к параметру t |
||
| прямой | общее уравнение |
Ax+By+C=0, где А и В координаты нормального вектора а(А,В). | Ах + By = О (С = 0) — прямая проходит через начало координат; Ах + С = 0 (В = 0) — прямая параллельна оси Оу; By + С = 0 (А = 0) — прямая параллельна оси Ох; Ах = О (В = С = О) — прямая совпадает с осью Оу; By = О (А = С = 0) — прямая совпадает с осью Ох. |
|
| прямой | уравнение в отрезках | в общем уравнении прямой на плоскости перенести свободный член направо и разделить все уравнение на этот свободный член. | ||
| плоскости | через три точки | 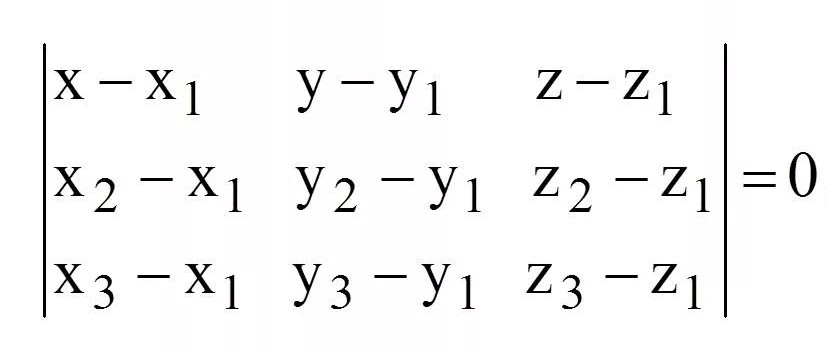 |
это основная матрица и способ для составления уравнения плоскости. При всех видах данных всегда ищите координаты трех точек, тогда уравнение плоскости составиться быстро и правильно. |
|
| плоскости | проходит через М(х0, у0, z0) и перпендикулярно вектору n (A,B,C) | A(x-x0)+B(y-y0)+C(z-z0)+D=0. | ||
| плоскости | Общее уравнение | Ax+By+Cz=0, где n (A,B,C) — нормальный вектор (перпендикулярен плоскости) |
Ах + By + Cz = 0 (D — 0) — плоскость проходит через начало координат; Ах + By + D = 0 (С = 0) — плоскость параллельна оси Oz (аналогичный смысл имеют уравнения Ах + Cz + D = 0, By + Cz + .D = 0); Ax + #2/ = 0 (D = С = 0) — плоскость проходит через ось Oz (Ах + Cz + D = 0,By + Cz + D = 0 — через ось Оу и Ох соответственно); Ах + D = 0 (В = С = 0) — плоскость параллельна плоскости Oyz (Cz + D = 0, By + D = 0 — параллельно плоскости Оху и Oxz соответственно); Ах = 0, т. е. х = 0 (В = С — D = 0) — плоскость совпадает с плоскостью Oyz (у = 0, z = 0 — уравнения плоскостей Oxz и Оху соответственно). |
|
| плоскости | уравнение в отрезках, где a,b,c — точки пересечения плоскости с осями ординат |
x/a+y/b+z/c=1 | ||
| плоскости | Через две параллельные прямые в каноническом виде |
|
1) выписываем координаты двух точек, через которые проходят эти прямые; 2) чтобы найти координаты третьей точки, записываем одну из прямых в параметрическом виде, принимает t за любое удобное значение и находим координаты третьей точки; 3) составляем матрицу (из разности координат). |
|
| плоскости | через точку А и прямую |
|
Из уравнения прямой выписываем координаты направляющего вектора и точки, через которую она проходит (пусть М). 3.2. Находим координаты вектора АМ (вычитаем соответствующие координаты). 3.3. Составляем матрицу, где х1,у1,z1 — координаты точки М, вторая строка координаты АМ, третья строка координаты направляющего вектора |
|
| плоскости | через пересекающиеся прямые |
|
Выписываем из уравнения прямых координаты точек, через которые они проходят. 4.2. Одну из прямых переписываем в параметрическом виде, принимаем t за удобное значение, находим координаты точки. 4.3. Важно, чтобы все эти точки были разными. 4.4. Важно, чтобы выбранные точки первой прямой не принадлежали второй, и наоборот. Поэтому берем точки первой прямой и подставляем в уравнение второй прямой, равенство должно нарушится. Повторяем процедуру для точки со второй прямой. 4.5. Составляем основную матрицу плоскости |
|
| плоскости | через точку М, перпендикулярно прямой l | 1.Выписываем координаты направляющего вектора прямой. Они являются координатами нормального вектора плоскости (так как по условию прямая и плоскость перпендикулярны).
2.Записываем уравнение плоскости A(x-x0)+B(y-y0)+C(z-z0)=0, где А,В,С — координаты нормального вектора, х0,у0,z0 — координаты заданной точки. |
||
| плоскости | через прямую и параллельную другой прямой |
|