Задание № 9
— ЕГЭ — профиль —
Исследование функции:
- базовый уровень сложности;
- рекомендуемое время выполнения — 3 минуты;
- за верное решение можно получить 1 балл;
- решение не проверяется, на апелляцию не подается;
- новое задание.
Графики учатся строить с седьмого класса. Ежегодно добавляется новая информация, но для решения этого задания требуется очень небольшой объем знаний. Поэтому Вы быстро восстановите нужные правила.
Информация для учеников. Как работать с материалом, размещенным в этом разделе?
1шаг. Выучите алгоритм и не отклоняйтесь от него!
2 шаг. Потренируйтесь в решении дополнительных заданий. Решайте их по алгоритму, отработайте алгоритм так, чтобы выполнять его не задумываясь.
Информация для родителей. Как работать с материалом, размещенным в этом разделе?
Уважаемые неравнодушные и беспокоящиеся родители  !
!
Если Вы хотите проконтролировать уровень своего ребенка или помочь ему в изучении методики решения этого задания, то
-
попросите ученика без каких-либо дополнительных повторений воспроизвести алгоритм;
-
попросите ученика решить самостоятельно размещенные на сайте образцы. Вы сможете проверить решение по размещенным здесь образцам. Просите ребенка, чтобы он объяснял каждый свой шаг, чтобы избежать механического запоминания образца решения. Ведь этот же самый алгоритм нужно будет повторить в задании с другими числами, размещенными в уравнении по другому, а значит нужно запомнить пошаговую логику, а не перемещение символов.
Дополнение:
Можно ли «совсем не разбираться в графиках и их не понимать»? Нельзя. Это очень легкий материал. И не вводите родителей в заблуждение.
Алгоритмы решения
Как найти f(x), если известен х
1.Считаем количество коэффициентов в заданном уравнении.
2.Находим координаты удобных точек графика. Сколько коэффициентов, столько точек.
3.Подставляем в заданное уравнение найденные координаты. Получаем систему уравнений. Сколько коэффициентов, столько уравнений.
4.Решаем систему уравнений любым доступным способом (не важно насколько он рационален или крут). Находим все коэффициенты.
5.Подставляем найденные коэффициенты в заданное уравнение. Получаем уравнение функции, которую нам задали.
6.Подставляем в уравнение функции заданный х. Если заданное число написано в скобках, то это х, в противном случае это у.
7. Вычисляем, выписываем ответ.
Как найти f(x), если известен у
1.Считаем количество коэффициентов в заданном уравнении.
2.Находим координаты удобных точек графика. Сколько коэффициентов, столько точек.
3.Подставляем в заданное уравнение найденные координаты. Получаем систему уравнений. Сколько коэффициентов, столько уравнений.
4.Решаем систему уравнений любым доступным способом (не важно насколько он рационален или крут). Находим все коэффициенты.
5.Подставляем найденные коэффициенты в заданное уравнение. Получаем уравнение функции, которую нам задали.
6.Подставляем в уравнение функции заданный заданный у. Если заданное число написано в скобках, то это х, в противном случае это у.
7. Вычисляем, выписываем ответ.
Как найти любой коэффициент в заданной формуле
1.Считаем количество коэффициентов в заданном уравнении.
2.Находим координаты удобных точек графика. Сколько коэффициентов, столько точек.
3.Подставляем в заданное уравнение найденные координаты. Получаем систему уравнений. Сколько коэффициентов, столько уравнений.
4.Решаем систему уравнений любым доступным способом (не важно насколько он рационален или крут). Находим все коэффициенты.
5.Выбираем нужный, выписываем ответ.
Как найти координату точки пересечения графиков
1.Считаем количество коэффициентов в заданном уравнении.
2.Находим координаты удобных точек графика. Сколько коэффициентов, столько точек.
3.Подставляем в заданное уравнение найденные координаты. Получаем систему уравнений. Сколько коэффициентов, столько уравнений.
4.Решаем систему уравнений любым доступным способом (не важно насколько он рационален или крут). Находим все коэффициенты.
5.Подставляем найденные коэффициенты в заданное уравнение. Получаем уравнение функции, которую нам задали.
6.Подставляем в уравнение функции заданный х или заданный у. Если заданное число написано в скобках, то это х, в противном случае это у.
7. Приравниваем уравнения, переносим все в одну сторону, решаем.
8. Выписываем ответ.
Правила
— учим —
-не читаем! не смотрим! учим!-
Выбираем точки
- точка должна находится на графике;
- точка должна находится на пересечении линий клеток;
- у каждой точки две координаты: первая — абсцисса (х); вторая — ордината (у);
- в записи f(x), f — это у;
- если в условии есть запись f(3), то известен х;
- если в условии есть запись f(x)=3, то известен у.
Стандартный вид прямой.
- у=кх+в — графиком всегда является прямая;
- х и у — это координаты точек графика, Вы будете определять их по чертежу;
- к и в — коэффициенты, которые Вы будете находить из системы уравнений;
- коэффициентов два, поэтому нужно найти координаты двух точек, система уравнений будет состоять из двух уравнений.
Стандартный вид параболы.
- у=ах²+вх+с — графиком всегда является парабола;
- х и у — это координаты точек графика, Вы будете определять их по чертежу;
- а, в и с — коэффициенты, которые Вы будете находить из системы уравнений;
- коэффициентов три, поэтому нужно найти координаты трех точек, система уравнений будет состоять из трех уравнений.
Стандартный вид гиперболы.
-
![Rendered by QuickLaTeX.com \[ y=\frac{k}{x+b}+c\]](https://learn-to-learn.com/wp-content/ql-cache/quicklatex.com-d4322663e1eb8a175e540dd893dffd0d_l3.png)
;
- х и у — это координаты точек графика, Вы будете определять их по чертежу;
- к,b и с — коэффициенты, которые Вы будете находить из системы уравнений;
- коэффициентов три, поэтому нужно найти координаты трех точек, система уравнений будет состоять из трех уравнений.
Стандартный вид графика модуля.
- у=|kx+b|+c;
- х и у — это координаты точек графика, Вы будете определять их по чертежу;
- к,b и с — коэффициенты, которые Вы будете находить из системы уравнений;
- коэффициентов три, поэтому нужно найти координаты трех точек, система уравнений будет состоять из трех уравнений.
Стандартный вид графика логарифма и степени.
- y=c+logax; у=ах+в;
- х и у — это координаты точек графика, Вы будете определять их по чертежу;
- а и с — коэффициенты, которые Вы будете находить из системы уравнений;
- коэффициентов два, поэтому нужно найти координаты двух точек, система уравнений будет состоять из двух уравнений.
Стандартный вид тригонометрических функций.
- у=acosx+b; y=asinx+b; y=atgx+b;
- х и у — это координаты точек графика, Вы будете определять их по чертежу;
- а и b — коэффициенты, которые Вы будете находить из системы уравнений;
- коэффициентов два, поэтому нужно найти координаты двух точек, система уравнений будет состоять из двух уравнений.
Способы решения системы уравнений (от количества уравнений не зависит).
- метод подстановки: выразить из одного из уравнений одну переменную и подставить это выражение в другое уравнение (можно использовать всегда);
- метод сложения (вычитания): сложить (вычесть) почленно одно уравнение с другим (удобно, если при этом одна из переменных уничтожится);
- домножение с последующим сложением (вычитанием): домножить одно (или оба уравнения) на такие числа, чтобы при дальнейшем сложении или вычитании одна из переменных уничтожилась.
Как находить точку пересечения?
Образцы решения
— учим —
-не читаем! не смотрим! учим!-
1.На рисунке изображён график функции вида f(x)=ах²+bx+c, где числа a, b и c — целые. Найдите f(-12).
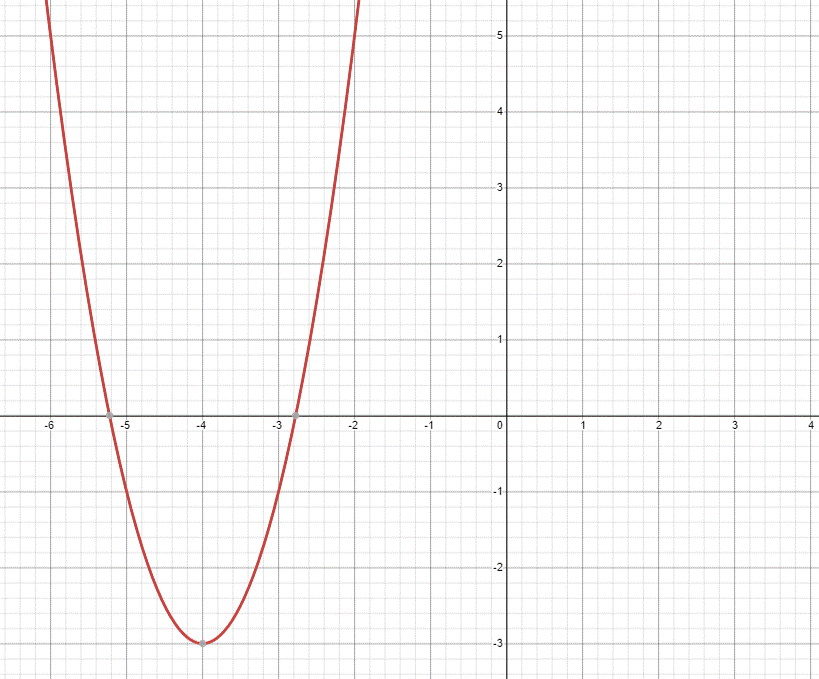
1.В уравнении три коэффициента: a,b,c.
2.Находим координаты трех точек: А(-3;-1); В(-5;-1); С(-4;-3).
3.Составляем систему уравнений:
![Rendered by QuickLaTeX.com \[ \left\{\begin{matrix} -1=9a-3b+c & & \\ -1=25a-5b+c & & \\ -3=16a-4b+c & & \end{matrix}\right.\]](https://learn-to-learn.com/wp-content/ql-cache/quicklatex.com-efe210ce1c72a063ab33a81a9ed2298b_l3.png)
Вычтем из первого второе, вычтем из первого третье, получим
![Rendered by QuickLaTeX.com \[ \left\{\begin{matrix} 0=-16a+2b=0 & & \\ 2=-7a+b & & \end{matrix}\right.\]](https://learn-to-learn.com/wp-content/ql-cache/quicklatex.com-4c6774e81669c6fb157079307802f6aa_l3.png)
Получим, а=2, b=16. Подставим эти значения в первое уравнение системы и найдем с. С=29.
4.Подставим все найденные коэффициенты в стандартный вид параболы, получим уравнение параболы: у=2х²+16х+19.
5.По условию известно, что х=-12, подставим это значение и найдем у: у=2•144+16•(-12)+19=288-192+19=115.
Ответ: 115.
2.На рисунке изображён график функции вида f(x)=ах²+bx+c, где числа a, b и c — целые. Найдите значение х, при котором f(х)=5. Если таких значений два, то в ответе запишите меньшее.

1.В уравнении три коэффициента: a,b,c.
2.Находим координаты трех точек: А(-3;-1); В(-5;-1); С(-4;-3).
3.Составляем систему уравнений:
![Rendered by QuickLaTeX.com \[ \left\{\begin{matrix} -1=9a-3b+c & & \\ -1=25a-5b+c & & \\ -3=16a-4b+c & & \end{matrix}\right.\]](https://learn-to-learn.com/wp-content/ql-cache/quicklatex.com-efe210ce1c72a063ab33a81a9ed2298b_l3.png)
Вычтем из первого второе, вычтем из первого третье, получим
![Rendered by QuickLaTeX.com \[ \left\{\begin{matrix} 16a-2b=0 & & \\ 2=-7a+b & & \end{matrix}\right.\]](https://learn-to-learn.com/wp-content/ql-cache/quicklatex.com-e3ed2b994c43b180ba388cca835e140b_l3.png)
Получим, а=2, b=16. Подставим эти значения в первое уравнение системы и найдем с. С=29.
4.Подставим все найденные коэффициенты в стандартный вид параболы, получим уравнение параболы: у=2х²+16х+19.
5.По условию известно, что у=5, подставим это значение и найдем х: 5=2х²+16х+19.
2х²+16х+19=5
2х²+16х+14=0, то есть х=-1 и х=-7. В ответе запишу меньшее значение.
Ответ: -7.
3.На рисунке изображён график функции вида f(x)=ах²+bx+c, где числа a, b и c — целые. Найдите значение b.

1.В уравнении три коэффициента: a,b,c.
2.Находим координаты трех точек: А(-3;-1); В(-5;-1); С(-4;-3).
3.Составляем систему уравнений:
![Rendered by QuickLaTeX.com \[ \left\{\begin{matrix} -1=9a-3b+c & & \\ -1=25a-5b+c & & \\ -3=16a-4b+c & & \end{matrix}\right.\]](https://learn-to-learn.com/wp-content/ql-cache/quicklatex.com-efe210ce1c72a063ab33a81a9ed2298b_l3.png)
Вычтем из первого второе, вычтем из первого третье, получим
![Rendered by QuickLaTeX.com \[ \left\{\begin{matrix} 16a-2b=0 & & \\ 2=-7a+b & & \end{matrix}\right.\]](https://learn-to-learn.com/wp-content/ql-cache/quicklatex.com-e3ed2b994c43b180ba388cca835e140b_l3.png)
Получим, а=2, b=16.
Ответ: 16.
На рисунке изображён график функции вида
![]()
где числа a, b и c — целые. Найдите f(-1/2).
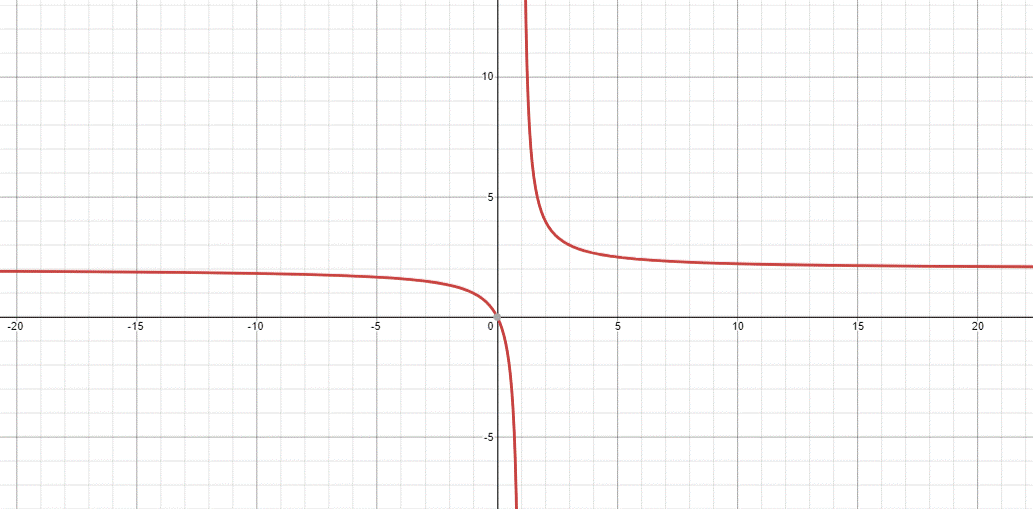
1.В уравнении три коэффициента: a,b,c.
2.Находим координаты трех точек: А(0;0); В(3;3); С(2;4).
3.Составляем систему уравнений:
0=a/b +c
3=a/(3+b) +c
4=a/(2+b) +c
Приведем к общему знаменателю:
а=-bc
а=(3+b)(3-c)
а=(2+b)(4-c)
Раскроем скобки, заменим во втором и третьем -bc на а, получим
3=с-b
4=c-2b
Получим, c=2, b=-1. Подставим эти значения в первое уравнение системы и найдем a. a=29.
4.Подставим все найденные коэффициенты в стандартный вид гиперболы, получим уравнение гиперболы:
![]()
5.По условию известно, что х=-1/2, подставим это значение и найдем у: у=1,5.
Ответ: 1,5.
На рисунке изображён график функции f(x)=kx+b. Найдите f(-10).
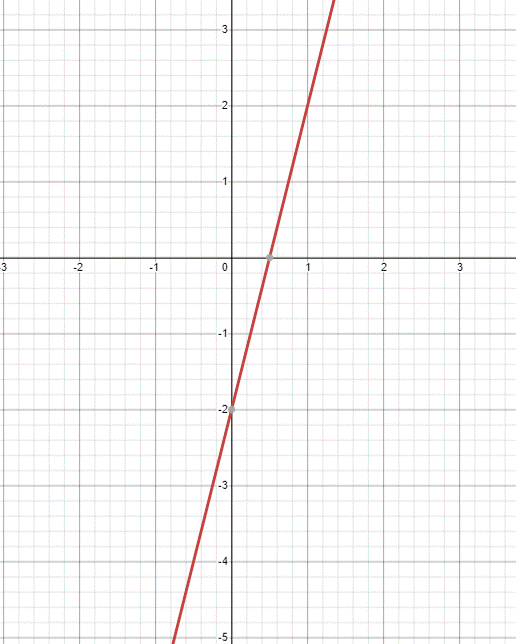
1.В уравнении два коэффициента k,b.
2.Находим координаты двух точек: А(0;-2); В(1;2).
3.Составляем систему уравнений:
-2=b
2=k+b
Подставим значение b из первого уравнения во второе, найдем k. К=4.
4.Подставим все найденные коэффициенты в стандартный вид прямой, получим уравнение прямой: f(x)=4x-2.
5.По условию известно, что х=-10, подставим это значение и найдем у: у=-42.
Ответ: -42.
На рисунке изображён график функции f(x)=acosx+b. Найдите f(10π/3).
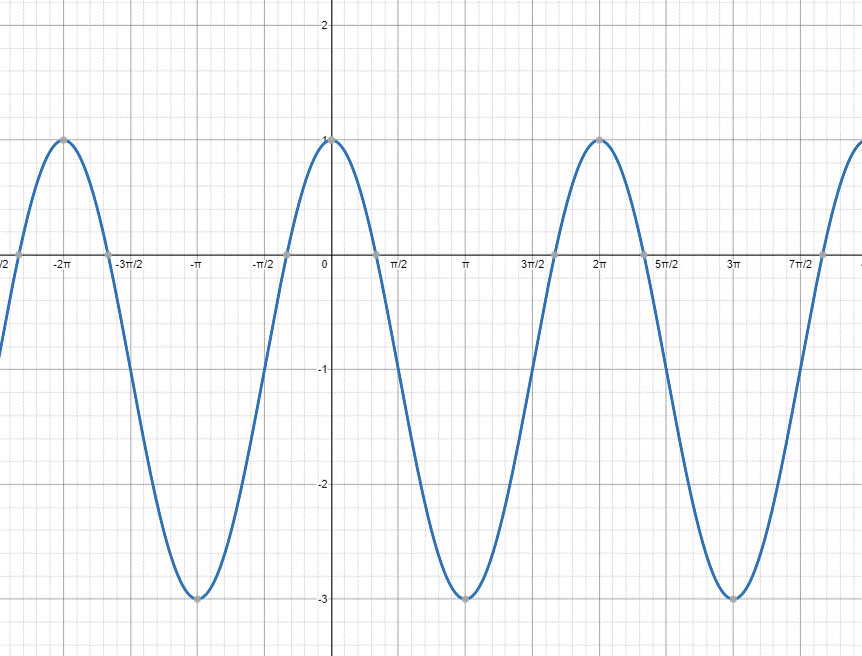
1.В уравнении два коэффициента а,b.
2.Находим координаты двух точек: А(0;1); В(π;-3).
3.Составляем систему уравнений:
1=а+b
-3=-а+b
Складываем уравнения, получаем, что 2b=-2, то есть b=-1.
Подставим значение b в первое уравнение, найдем а. а=2.
4.Подставим все найденные коэффициенты в стандартный вид функции косинуса, получим уравнение: f(x)=2cosx-1.
5.По условию известно, что х=10π/3, подставим это значение и найдем у: у=-2.
Ответ: -2.
На рисунке изображен график функции f(x)=|kx+b|+c, найдите значение f(-20).
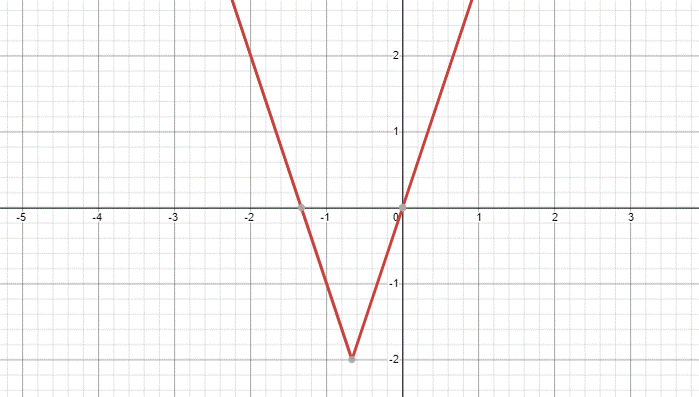
1.В уравнении три коэффициента k,b,c.
2.Находим координаты трех точек: А(0;0); В(-1;-1), С(-2;2).
3. Раскрываем модуль, чтобы уравнение приобрело более простой вид:
(1) у=кх+b+c и (2) y=-kx-b+c.
Подставляем координаты точки А в (1) уравнение, так как эта точка лежит на возрастающей части графика. Подставляем координаты точек В и С во (2) уравнение, так как они лежат на убывающей части графика. Составляем систему уравнений:
0=b+с (1)
-1=k-b+c (2)
2=2k-b+c (3)
Вычитаем из (3) уравнения (2), получаем, что к=3.
Подставляем К во второе уравнение, складываем его с первым, находим с=-2, b=2.
4.Подставим все найденные коэффициенты в стандартный вид, получим уравнение: f(x)=|3x+2|-2.
5.По условию известно, что х=-20, подставим это значение и найдем у: у=56.
Ответ: 56.