Задание № 15
— ЕГЭ — профиль —
Экономическая задача:
- рекомендуемое время выполнения — 20 минут;
- за верное решение можно получить — 2 балла;
- решение проверяется, можно подать на апелляцию;
- все необходимые знания и умения формируются в 8-11 классах;
- Внимание: в тексте встречается «задание № 17» — это прошлогодняя нумерация. Номер задания поменялся, но содержания задания и алгоритмы решения остались.
Информация для учеников. Как работать с материалом, размещенным в этом разделе?
1шаг. Обязательно выучить всю теорию. Не тратьте время на попытки решить наугад. Время дорого!
2 шаг. Внимательно изучите все образцы решения. Попробуйте самостоятельно воспроизвести эти решения по памяти. «По памяти» — не подглядывая, ни на секунду, ни «одним глазком», ни «чтобы просто убедиться». При решении заданий проговаривайте объяснение полностью.
3 шаг. Потренируйтесь в решении дополнительных заданий. Решайте их по алгоритму, отработайте алгоритм так, чтобы выполнять его не задумываясь.
Информация для родителей. Как работать с материалом, размещенным в этом разделе?
Уважаемые неравнодушные и беспокоящиеся родители  !
!
Если Вы хотите проконтролировать уровень своего ребенка или помочь ему в изучении методики решения этого задания, то
-
попросите ученика без каких-либо дополнительных повторений воспроизвести всю теорию. Проверять Вы его можете по тексту на сайте, Вам самим для этого не нужно изучать правила. Воспроизведение должно быть максимально полным и точным.
-
не задавайте наводящих вопросов. Как правило, Ваши вопросы — это скорее подсказки, а они нам не нужны. Пусть ребенок самостоятельно воспроизведет все правила, которые относятся к определенному типу заданий;
-
попросите ученика решить самостоятельно размещенные на сайте образцы. Вы сможете проверить решение по размещенным здесь образцам. Просите ребенка, чтобы он объяснял каждый свой шаг, чтобы избежать механического запоминания образца решения. Ведь этот же самый алгоритм нужно будет повторить в задании с другими числами, размещенными в уравнении по другому, а значит нужно запомнить пошаговую логику, а не перемещение символов.
Дополнение:
Можно ли учить не всю теорию? Нельзя.
Чем больше уравнений Вы прорешаете, тем быстрее правила закрепятся в памяти, поэтому практика, практика и еще раз практика.
Можно ли решать другим способом? Да, конечно. Если Ваш способ никогда Вас не подводит, то ни в коем случае от него не отказывайтесь, не переучивайтесь, у Вас и так все будет хорошо.
Правила по всем типам задач
1.Кредит — это некоторая сумма денег, которую мы берем в банке на время, ее нужно вернуть в определенный срок, указанный в договоре.
2.Вернуть банку мы должны не только сумму, которую взяли, но и банковские начисления. Чтобы найти общую сумму выплат, нужно к сумме кредита добавить ежегодные (или ежемесячные) банковские начисления.
3.Банковские начисления рассчитываются по формуле: банковский коэффициент умножить на сумму долга.
4.Банковский коэффициент равен банковскому проценту деленному на 100.
5.Наш долг перед банком меняется, поэтому и банковские начисления будут меняться.
6.В стандартном кредите самые большие банковские начисления в за первый период, так как банковский коэффициент умножается на всю сумму кредита.
7.Банк начисляет проценты не на сумму, которую мы взяли, а на наш долг в данный момент.
8.Чтобы погасить наш долг перед банком, мы ежемесячно (или ежегодно) выплачиваем некоторую сумму. Она может быть известна в задаче, а может быть неизвестна.
9. После последней выплаты наш долг будет равен 0.
10.При чтении задачи Вы должны найти информацию о сумме кредита, банковском проценте, выплатах, как изменяется долг, сроке кредита.
11.Величины, которые неизвестны, нужно обозначить переменными или составить для них выражения. Все обозначения должны быть грамотно оформлены в краткой записи задачи.
12.Мы не решаем задачи в процентах, поэтому банковский процент нужно разделить на 100, прежде чем использовать в решении.
13.Для решения задачи необходимо составить или уравнение, или систему уравнений, или неравенство.
14. Таблица для решения задач, в которых в условии указано, что «долг уменьшается на одну и ту же сумму».
| Год/месяц | Фиксированный платеж, млн рублей | Выплата банковских начислений |
15. Таблица для решения задач, в которых долг изменяется произвольным образом.
| Год/месяц | Долг в начале периода, млн рублей | Банковские начисления, млн рублей | Выплаты, млн рублей | Долг в конце периода, млн рублей |
16. Для задач с произвольным изменением долга составляем выражение:
долг в начале периода + банковские начисления — выплаты = долг в конце периода.
С помощью этого выражения мы можем найти неизвестные данные (в каждой задаче они свои).
Решение задач о кредитах (долг меняется на одну и ту же сумму)
Задача № 1
В июле планируется взять кредит в банке на сумму 6 млн рублей на срок 15 лет. Условия его возврата таковы:
- каждый январь долг возрастает на х% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
Найдите х, если известно, что наибольший платеж по кредиту составит не более 1,9 млн рублей, а наименьший — не менее 0,5 млн рублей?
Краткое содержание и анализ условия задачи:
- в банке берется кредит (деньги);
- сумма кредита — 6 млн.;
- срок кредита — 15 лет;
- важная фраза «долг уменьшается на одну и ту же сумму», поэтому решаем задачу с помощью таблицы выплат (всего три колонки);
- так как «долг уменьшается на одну и ту же сумму», то ежегодный платеж складывается из фиксированного платежа и выплаты банковских начислений за год (то есть ежегодная выплата состоит из двух частей);
- фиксированный платеж — часть кредита, которую мы выплачиваем каждый год (постоянно одна и та же сумма) = 6/15;
- вся сумма кредита делится на 15 лет на равные части; то есть каждый год долг уменьшается на 1/15 часть кредита;
- банковский процент не известен, в условии обозначен х%;
- для решения задачи нужен банковский коэффициент а= х/100 (всегда находится таким образом);
- каждый год банк начисляет свой процент на долг (на долг, а не на кредит);
- ежегодные банковские начисления рассчитываются по формуле: банковский коэффициент • на долг (на долг, а не на кредит);
- долг за 1 год равен всей сумме кредита, так как никаких выплат не было, и банк начислит свои проценты на всю сумму кредита, то есть на 6 млн рублей;
- долг каждый год разный, причина:
- банк увеличивает его на некоторый процент;
- мы постоянно выплачиваем кредит, поэтому долг уменьшается;
- максимальный ежегодный платеж будет в том году, когда долг был максимальным;
- минимальный ежегодный платеж будет в том году, когда долг был минимальным.
Решение:
Пусть а — повышающий коэффициент, а=х/100.
Так как долг должен уменьшаться на одну и ту же сумму, то ежегодные выплаты должны состоять из двух частей: фиксированного платежа, который равен 6/15, и выплаты ежегодных банковских начислений.
Так как мы ежегодно выплачиваем 6/15, то есть каждый год долг уменьшается на 1/15 часть кредита. Изменение долга по годам выглядит следующим образом:
| Год | Остаток долга |
| 1 | 6 |
| 2 | 6•14/15 |
| 3 | 6•13/15 |
| … | … |
| 15 | 6•1/15 |
Составим таблицу выплат:
| Год | Фиксированный платеж, млн рублей | Выплата банковских начислений, млн рублей |
| 1 | 6/15 | а•6 |
| 2 | 6/15 | а•6•14/15 |
| … | … | … |
| 15 | 6/15 | а•6•1/15 |
Максимальным будет первый платеж, так как долг за первый 1 год самый большой: 6/15 +6а≤1,9, то есть а≤0,25.
Минимальным будет последний платеж, так как долг за последний год самый маленький: 6/15 +6а/15≥0,5, то есть а≥0,25.
Следовательно, а=0,25. Подставляем вместо а х/100, находим, что х=25%.
Ответ:: 25%.
Задача № 2
В июле планируется взять кредит в банке на 15 лет. Условия его возврата таковы:
- каждый январь долг возрастает на х% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
Найдите х, если известно, что за весь период выплатили на 15% больше, чем взяли в кредит.
Краткое содержание и анализ условия задачи:
- в банке берется кредит (деньги);
- сумма кредита не известна, поэтому обозначаем ее S;
- срок кредита — 15 лет;
- важная фраза «долг уменьшается на одну и ту же сумму», поэтому решаем задачу с помощью таблицы выплат (всего три колонки);
- так как «долг уменьшается на одну и ту же сумму», то ежегодный платеж складывается из фиксированного платежа и выплаты банковских начислений за год (то есть ежегодная выплата состоит из двух частей);
- фиксированный платеж — часть кредита, которую мы выплачиваем каждый год (постоянно одна и та же сумма) = S/15;
- вся сумма кредита делится на 15 лет на равные части; то есть каждый год долг уменьшается на 1/15 часть кредита;
- банковский процент не известен, в условии обозначен х%;
- для решения задачи нужен банковский коэффициент а= х/100 (всегда находится таким образом);
- каждый год банк начисляет свой процент на долг (на долг, а не на кредит);
- ежегодные банковские начисления рассчитываются по формуле: банковский коэффициент • на долг (на долг, а не на кредит);
- долг в 1 год равен всей сумме кредита, так как никаких выплат не было, и банк начислит свои проценты на всю сумму кредита, то есть на S;
- долг каждый год разный, причина:
- банк увеличивает его на некоторый процент;
- мы постоянно выплачиваем кредит, поэтому долг уменьшается;
- по условию задачи общая сумма выплат больше суммы кредита на 15%, то есть общая сумма выплат равна 115% от суммы кредита;
- так как в решении задачи мы процентами не пользуемся, то общая сумма выплат равна 1,15S.
Решение:
Пусть а — повышающий коэффициент, а=х/100, S — сумма кредита.
Так как долг должен уменьшаться на одну и ту же сумму, то ежегодные выплаты должны состоять из двух частей: фиксированного платежа, который равен S/15, и выплаты ежегодных банковских начислений.
Так как мы ежегодно выплачиваем S/15, то есть каждый год долг уменьшается на 1/15 часть кредита. Изменение долга по годам выглядит следующим образом:
| Год | Остаток долга |
| 1 | S |
| 2 | S•14/15 |
| 3 | S•13/15 |
| … | … |
| 15 | S•1/15 |
Составим таблицу выплат:
| Год | Фиксированный платеж, млн рублей | Банковские начисления, млн рублей |
| 1 | S/15 | а•S |
| 2 | S/15 | а•S•14/15 |
| … | … | … |
| 15 | S/15 | а•S•1/15 |
Найдем общую сумму выплат.
- сложим все фиксированные платежи: 15•S/15=S (второй столбик);
- сложим все выплаты банковских начислений, то есть третий столбик. Для этого вынесем общий множитель a•S/15 за скобку, получим выражение
-
-
- Сумму в скобках найдем с помощью формулы для суммы арифметической прогрессии
-
- то есть сумма выплат банковских процентов равна
-
-
- тогда общая сумма выплат будет равна S+8aS.
По условию общая сумма выплат равна 1,15S. Составляем уравнение: S+8aS=1,15S, то есть а=3/160.
Подставляем вместо а — х/100, получаем, что х=1,875%.
Ответ:: 1,875%.
Задача № 3
В июле планируется взять кредит в банке на сумму 16 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
- каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
Насколько лет планируется взять кредит, если известно, что общая сумма выплат составит 38 млн рублей.
Краткое содержание и анализ условия задачи:
- в банке берется кредит (деньги);
- сумма кредита 16 млн рублей;
- срок кредита не известен, поэтому обозначим его за х (строго целое число);
- важная фраза «долг уменьшается на одну и ту же сумму», поэтому решаем задачу с помощью таблицы выплат (всего три колонки);
- так как «долг уменьшается на одну и ту же сумму», то ежегодный платеж складывается из фиксированного платежа и выплаты банковских начислений за год (то есть ежегодная выплата состоит из двух частей);
- фиксированный платеж — часть кредита, которую мы выплачиваем каждый год (постоянно одна и та же сумма) = 16/х;
- вся сумма кредита делится на 16 лет на равные части; то есть каждый год долг уменьшается на 1/х часть кредита;
- банковский процент составляет 25%;
- для решения задачи нужен банковский коэффициент а= 25/100=0,25 (всегда находится таким образом);
- каждый год банк начисляет свой процент на долг (на долг, а не на кредит);
- ежегодные банковские начисления рассчитываются по формуле: банковский коэффициент • на долг (на долг, а не на кредит);
- долг за 1 год равен всей сумме кредита, так как никаких выплат не было, и банк начислит свои проценты на всю сумму кредита, то есть на 16 млн рублей;
- долг каждый год разный, причина:
- банк увеличивает его на некоторый процент;
- мы постоянно выплачиваем кредит, поэтому долг уменьшается;
- по условию задачи всего мы банку выплатим 38 млн рублей.
Решение:
Пусть х — срок кредита.
Так как долг должен уменьшаться на одну и ту же сумму, то ежегодные выплаты должны состоять из двух частей: фиксированного платежа, который равен 16/х, и выплаты ежегодных банковских начислений.
Так как мы ежегодно выплачиваем 16/х, то есть каждый год долг уменьшается на 1/х часть кредита. Изменение долга по годам выглядит следующим образом:
| Год | Остаток долга |
| 1 | 16 |
| 2 | 16•(х-1)/х |
| 3 | 16•(х-2)/х |
| … | … |
| х | 16•1/х |
Составим таблицу выплат:
| Год | Фиксированный платеж, млн рублей | Банковские начисления, млн рублей |
| 1 | 16/х | 0,25•16 |
| 2 | 16/х | 0,25•16(х-1)/х |
| … | … | … |
| х | 16/х | 0,25•16•1/х |
Найдем общую сумму выплат.
- сложим все фиксированные платежи: х•16/х=16 (второй столбик);
- сложим все выплаты банковских начислений, то есть третий столбик. Для этого вынесем общий множитель 0,25•16/х за скобку, получим выражение
-
-
- Сумму в скобках найдем с помощью формулы для суммы арифметической прогрессии
-
- то есть сумма выплат банковских процентов равна
-
-
- тогда общая сумма выплат будет равна 16+2(x+1).
По условию общая сумма выплат равна 38 млн рублей. Составляем уравнение: 16+х(х+1)=38, то есть х=10.
Ответ:: 10.
Решения задач о кредитах
(долг меняется произвольным образом)
Задача 1
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца, где r — целое число;
- со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
- 15 числа каждого месяца долг должен составлять некоторую сумму в соответствии с таблицей
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 1 | 0,6 | 0,4 | 0,3 | 0,2 | 0,1 | 0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.
Краткое содержание и анализ условия задачи:
- в банке берется кредит (деньги);
- сумма кредита 1 млн рублей;
- срок кредита 6 месяцев;
- долг меняется произвольным образом
- банковский процент не известен, обозначен за r%;
- для решения задачи нужен банковский коэффициент а= r/100 (всегда находится таким образом);
- каждый месяц банк начисляет свой процент на долг (на долг, а не на кредит);
- ежемесячные банковские начисления рассчитываются по формуле: банковский коэффициент • на долг (на долг, а не на кредит);
- долг за 1 месяц равен всей сумме кредита, так как никаких выплат не было, и банк начислит свои проценты на всю сумму кредита, то есть на 1 млн рублей;
- долг каждый год разный, причина:
- банк увеличивает его на некоторый процент;
- мы постоянно выплачиваем кредит, поэтому долг уменьшается;
- схема изменения долга задана в условии;
- по условию задачи всего мы банку выплатим менее 1,2 млн рублей.
Решение:
Пусть а — банковский коэффициент = r/100, х1, х2, х3, х4, х5, х6 — соответствующие ежемесячные платежи.
Заполняем таблицу:
| месяц | Долг в начале периода, млн рублей | Банковские начисления, млн рублей | Выплаты, млн рублей | Долг в конце периода, млн рублей |
| 1 | 1 | а•1 | х1 | 0,6 |
| 2 | 0,6 | 0,6а | х2 | 0,4 |
| 3 | 0,4 | 0,4а | х3 | 0,3 |
| 4 | 0,3 | 0,3а | х4 | 0,2 |
| 5 | 0,2 | 0,2а | х5 | 0,1 |
| 6 | 0,1 | 0,1а | х6 | 0 |
Для каждого месяца (для каждой строки) составляем выражение:
долг в начале периода + банковские начисления — выплаты = долг в конце периода
1 месяц: 1+а — х1 =0,6, отсюда выплата в 1 месяце х1 = 0,4+а;
2 месяц: 0,6+0,6а- х2=0,4, отсюда выплата во 2 месяце х2= 0,2+0,6а;
3 месяц: 0,4 + 0,4а — х3=0,3, отсюда выплата в 3 месяце х3= 0,1+0,4а;
4 месяц: 0,3 +0,3а- х4= 0,2, отсюда выплата в 4 месяце х4=0,1+0,3а;
5 месяц: 0,2+0,2а- х5=0,1, отсюда выплата в 5 месяце х5 =0,1+0,2а;
6 месяц: 0,1+0,1а -х6 =0, отсюда выплата в 6 месяце х6 = 0,1+0,1а.
Найдем общую сумму выплат, сложим все х:
0,4+а+0,2+0,6а+0,1+0,4а+0,1+0,3а+0,1+0,2а+0,1+0,1а=1+2,6а.
По условию задачи общая сумма выплат должна быть меньше 1,2 млн рублей, поэтому 1+2,6а<1,2, поэтому а<1/13.
Подставим вместо а r/100, получим r<100/13, то есть r должен быть меньше 7 с остатком. Так как по условию r целое число, то наибольшее возможное значение r это 7.
.Ответ:: 7.
Задача 2
15-го января планируется взять кредит в банке на три года в размере S млн рублей, где S — целое число. Условия его возврата таковы:
- каждый январь долг увеличивается на 25% по сравнению с концом предыдущего месяца, где r — целое число;
- с февраля по июнь каждого месяца необходимо выплатить часть долга;
- в июле каждого года долг должен составлять некоторую сумму в соответствии с таблицей
| год | июль 2016 | июль 2017 | июль 2018 | июль 2019 |
| Долг (в млн рублей) | S | 0,7S | 0,4S | 0 |
Найдите наименьшее значение S, при котором каждая из выплат будет больше 5 млн рублей.
Краткое содержание и анализ условия задачи:
- в банке берется кредит (деньги);
- сумма кредита S млн рублей (строго целое число);
- срок кредита 3 года;
- банковский процент составляет 25%;
- для решения задачи нужен банковский коэффициент а= 25/100=0,25 (всегда находится таким образом);
- каждый год банк начисляет свой процент на долг (на долг, а не на кредит);
- ежегодные банковские начисления рассчитываются по формуле: банковский коэффициент • на долг (на долг, а не на кредит);
- долг за первый год равен всей сумме кредита, так как никаких выплат не было, и банк начислит свои проценты на всю сумму кредита, то есть на S млн рублей;
- долг каждый год разный, причина:
- банк увеличивает его на некоторый процент;
- мы постоянно выплачиваем кредит, поэтому долг уменьшается;
- наименьшей выплатой будет та, где долг меньше всего;
- по условию задачи каждая выплата (не общая!) больше 5 млн рублей, это возможно, если наименьшая выплата будет больше 5 млн рублей.
Решение:
Пусть х1, х2, х3 — соответствующие ежемесячные платежи.
Составим таблицу:
| год | Долг в начале периода, млн рублей | Банковские начисления, млн рублей | Выплаты, млн рублей | Долг в конце периода, млн рублей |
| 1 | S | 0,25•S | х1 | 0,7S |
| 2 | 0,7S | 0,25•0,7S | х2 | 0,4S |
| 3 | 0,4S | 0,25•0,4S | х3 | 0 |
Для каждого года (для каждой строки) составляем выражение:
долг в начале периода + банковские начисления — выплаты = долг в конце периода
1 год: S+0,25S — х1 =0,7S, отсюда выплата в 1 месяце х1 = 0,55S;
2 год: 0,7S+0,175S- х2=0,4S, отсюда выплата во 2 месяце х2= 0,475S;
3 год: 0,4S + 0,1S — х3=0, отсюда выплата в 3 месяце х3= 0,5S.
Нас интересует наименьшая выплата — это выплата за 2-ой год: 0,475S>5, то есть S>200/19 (или 10 с остатком 10). Так как по условию S наименьшее целое число, то S=11.
Ответ:: 11.
Задача 3 /чтобы увеличить изображение, нажмите на него/
Задачи 4-5-6 /чтобы увеличить изображение, нажмите на него/
Задача 7 /чтобы увеличить изображение, нажмите на него/
Задача 8 /чтобы увеличить изображение, нажмите на него/
Задача 9 /чтобы увеличить изображение, нажмите на него/
Решение задач о производстве, предпринимателях
Задача 1
Антон является владельцем двух заводов в разных городах. На заводах производится абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара.
За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, — 200 рублей.
Антон готов выделять 900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Решение:
1.Ввожу необходимые переменный: пусть
- к- общее количество единиц товара,
- х — количество товара, произведенного на первом заводе, тогда х² — суммарное время работы на первом заводе, на оплату работы будет потрачено 250х²;
- у-количество товара, произведенного на втором заводе, тогда у² — суммарное время работы на втором заводе, на оплату труда будет потрачено 200у²;
- всего будет потрачено 250х²+200у²=900000, а всего произведено к=х+у;
- тогда, 250(к-у)²+200у²=900000
-
-
- 9у²-10ку+4у²-18000=0
- D=100k²-4·9(4y²-18000)
- уравнение имеет решение, если D≥0, поэтому 100k²-4·9(4y²-18000)≥0
- то есть -90≤к≤90, так как нас интересует максимальное целое значение к, то к=90.
-
-
Ответ: 90.
Задача 2
У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 500 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором — 500 ц/га.
Фермер может продать картофель по цене 5000 руб. за центнер, а свёклу — по цене 8000 руб. за центнер. Какой наибольший доход может получить фермер?
Решение:
1.Вижу, что на втором поле нужно выращивать свеклу, так как ее урожайность там выше, и стоимость свеклы больше.
- со второго поля доход составит 8000·500·10=40000000;
2.Первое поле
- сажаем свеклу, то доходность будет 8000·300·10=24000000;
- сажаем картошку, то доходность будет 5000·500·10=25000000;
- сажаем и картошку, и свеклу, сможем ли получить больше 25000000?:
- пусть х=количество га картошки, 10-х — количество га свеклы, тогда 5000·500·х+8000·300·(10-х)>25000000, если х>10, а это не возможно, так как все поле занимает 10 га;
- то есть максимальный доход с первого поля 25000000 (сажаем только картошку).
3. Общий доход: 40000000+25000000=65000000.
Ответ: 65000000.
Задача 3
Задача 4
Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 30 квадратных метров и номера «люкс» площадью 40 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 940 квадратных метров. Предприниматель может определить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 4000 рублей в сутки, а номер «люкс» — 5000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?
Решение:
Введу переменные для неизвестных величин:
- количество стандартных номеров — х, если все номера в гостинице будут такими, то их будет 940/30=31, а максимальный доход составит 31·4000=124000; (10 м² будет не использовано);
- количество «люксов» — у, если все номера будут такими, то их будет 940/40=23, а максимальный доход составит 23·5000=115000 (20м² будет не использовано);
Возможно ли получить больший доход, чем 124000 рублей, если в гостинице будут номера обеих категорий:
- 4000х+5000у>124000, при условии, что 30х+40у≤940,
- то есть 4х+5у>124, при условии, что 3х+4у≤94;
- домножим первое неравенство на -3 (не забудьте перевернуть знак неравенства), второе неравенство домножим на 4; сложим получившиеся неравенства
- у<4;
- проверим, при каких у от 1 до 3 получается максимальная прибыль;
- при у=1 прибыль максимальна: 5000+30·4000=125000.
Ответ: 125 000 рублей.
Задача 5
В двух шахтах добывают алюминий и никель. В первой шахте имеется 20 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1 кг алюминия или 2 кг никеля. Во второй шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 2 кг алюминия или 1 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
Решение:
Тренировочные задания
Задача 1
В июле 2026 года планируется взять кредит в банке на пять лет в размере S тыс. рублей. Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле 2027, 2028 и 2029 долг остаётся равным S тысяч рублей;
— выплаты в 2030 и 2031 годах равны по 360 тысяч рублей;
— к июлю 2031 долг будет выплачен полностью.
Найдите общую сумму выплат за пять лет.
Ответ: 1050 тыс. руб.
Задача 2
В июле 2026 года планируется взять кредит на пять лет в размере S тыс. рублей. Условия его возврата таковы:
— каждый январь долг возрастает на 30% по сравнению с концом предыдущего года;
— в июле 2027, 2028 и 2029 годов долг остается равным S тыс. рублей;
— выплаты в 2030 и 2031 годах равны по 338 тыс. рублей;
— к июлю 2031 года долг будет выплачен полностью. Найдите общую сумму выплат за пять лет.
Ответ: 1090 тыс.рублей.
Задача 3
Был выдан кредит на 550 000 рублей. Известно, что банк каждый год увеличивает сумму кредита на 20%, после чего происходит платеж. Кредит был полностью выплачен за 2 года, причем платежи были равны. Найдите общую сумму, выплаченную клиентом банку.
Ответ: 720 000 рублей.
Задача 4
Был выдан кредит на 250 000 рублей. Известно, что банк каждый год увеличивает сумму кредита на r%, после чего происходит платеж. Кредит был полностью выплачен за 2 года. Найдите r, если первый платеж составил 150 000 рублей, а второй 180 000 рублей.
Ответ: 20%.
Задача 5
Был выдан кредит на 400 000 рублей. Известно, что банк каждый год увеличивает сумму кредита на r%, после чего происходит платеж. Кредит был полностью выплачен за 2 года. Найдите r, если первый платеж составил 330 000 рублей, а второй 121 000 рублей.
Ответ: 10%.
Задача 6
Был выдан кредит на 300 000 рублей. Известно, что банк каждый год увеличивает сумму кредита на r%, после чего происходит платеж. Кредит был полностью выплачен за 2 года. Найдите r, если первый платеж составил 260 тыс. рублей, а второй — 169 000 рублей.
Ответ: 30%.
Задача 7
В июле планируется взять кредит в банке на сумму 5 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 7,5 млн рублей?
Ответ: 4.
Задача 8
Планируется открыть вклад на 4 года, положив на счет целое число млн рублей. В конце каждого года он увеличивается на 10%, а в начале третьего и четвертого года вклад пополняется на 5 млн рублей. Найдите наименьший первоначальный вклад, при котором начисленные проценты за весь срок будут более 10 млн рублей.
Ответ: 19 млн рублей.
Задача 9
Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме этого, в начале третьего и четвертого годов вкладчик ежегодно пополняет вклад на 10 млн рублей. Найдите наибольший размер первоначального вклада, при котором банк за четыре года начислит на вклад меньше 15 млн рублей.
Ответ: 25 млн рублей.
Задача 10
Планируется открыть вклад на 4 года, положив на счет целое число миллионов рублей. В конце каждого года сумма, лежащая на вкладе, увеличивается на 10%, а в начале третьего и четвертого года вклад пополняется на 3 миллиона рублей. Найдите наименьший первоначальный вклад, при котором начисленные проценты за весь срок будут более 5 миллионов рублей.
Ответ: 9 млн рублей.
Задача 11
В июле планируется взять кредит в банке на сумму 18 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если общая сумма выплат после полного погашения кредита составила 27 млн рублей?
Задача 12
Взяли кредит 177 120 рублей в банке на четыре года под 25% годовых и выплатили четырьмя равными платежами.
Чему будет равна общая сумма выплат после полного погашения кредита?
Задача 13
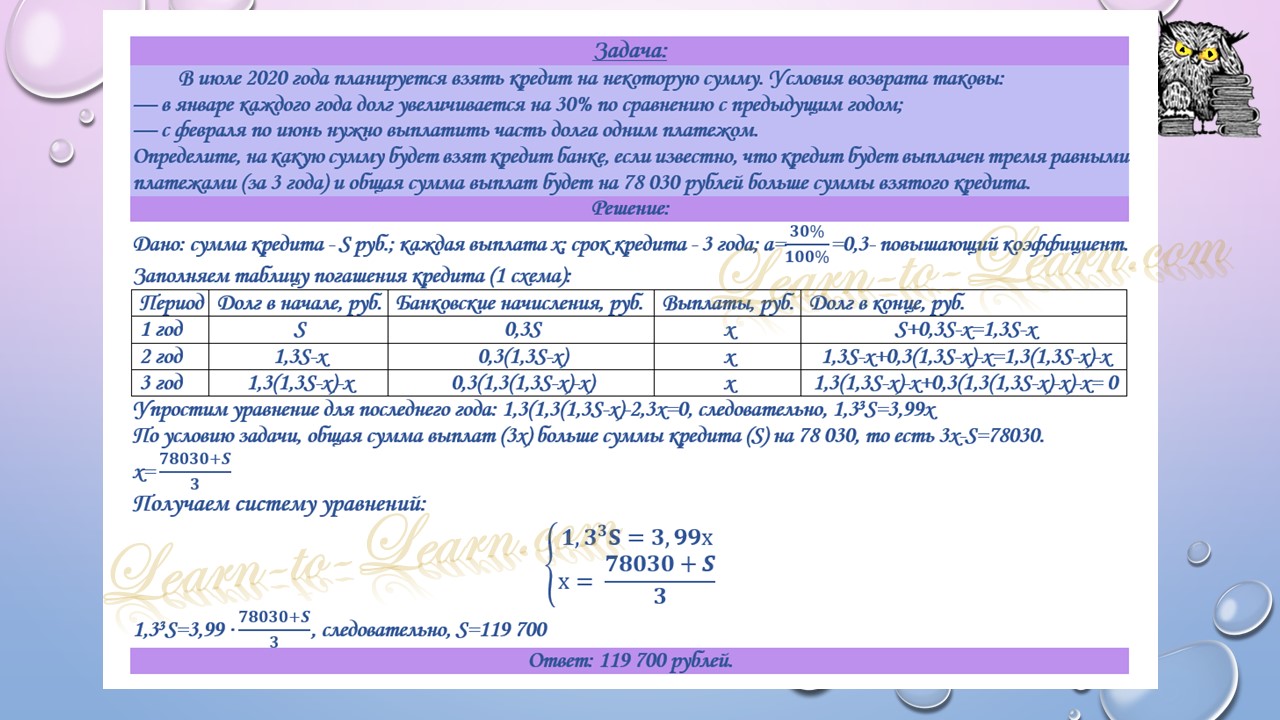
В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата таковы:
— в январе каждого года долг увеличивается на 30% по сравнению с предыдущим годом;
— с февраля по июнь нужно выплатить часть долга одним платежом.
Определите, на какую сумму взяли кредит банке, если известно, что кредит был выплачен тремя равными платежами (за 3 года) и общая сумма выплат на 156 060 рублей больше суммы взятого кредита.
Задача 14
Взяли кредит в банке на сумму 200 000 рублей под r% процентов годовых и выплатили за 2 года платежами 130 000 рублей в первый год и 150 000 рублей — во второй. Найдите r.
6. Взяли кредит в банке на сумму 250 000 рублей под r% процентов годовых и выплатили за 2 года платежами 150 000 рублей в первый год и 180 000 рублей — во второй.
Найдите r.
Задача 15
В августе 2020 года взяли кредит. Условия возврата таковы:
— в январе каждого года долг увеличивается на r%;
— с февраля по июль необходимо выплатить часть долга.
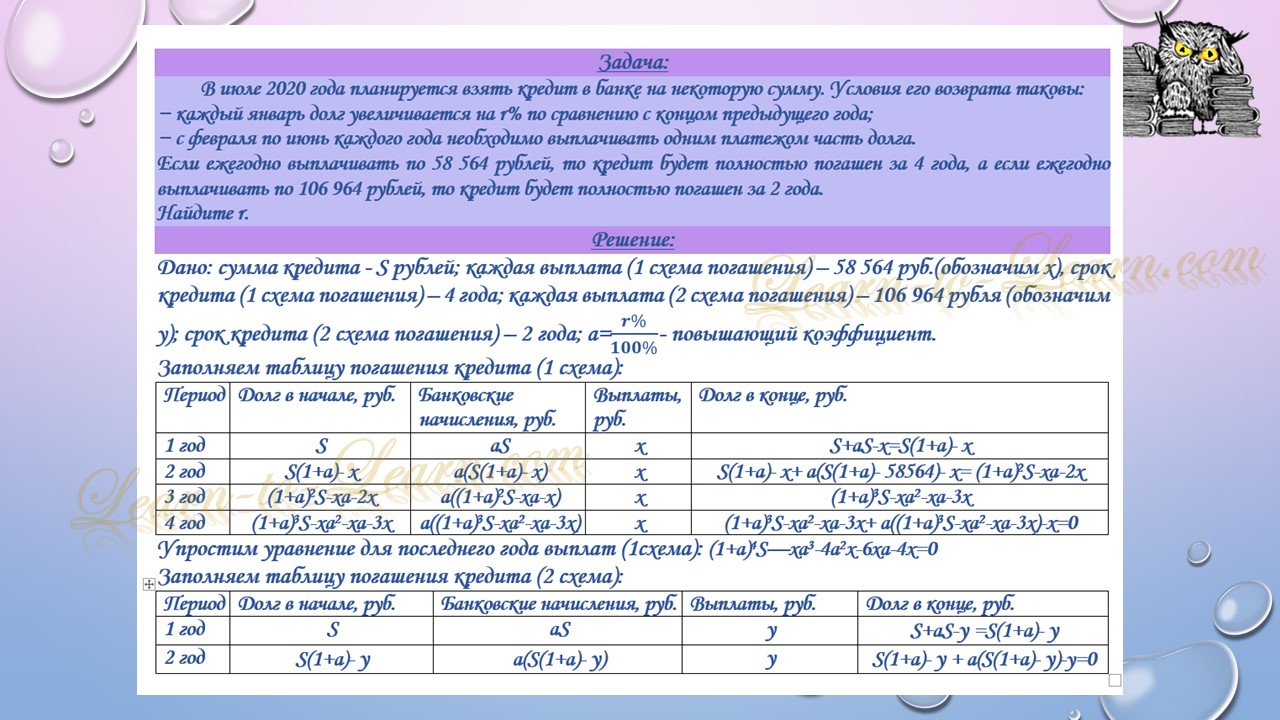
Кредит можно выплатить за четыре года равными платежами по 777 600 рублей, или за два года равными платежами по 1 317 600 рублей.
Найдите r.
Задача 16
15-го января планируется взять кредит в банке на несколько месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 5% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
На сколько месяцев можно взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 25% больше суммы, взятой в кредит.
Задача 17
15-го января планируется взять кредит в банке на некоторое количество месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возврастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
На сколько месяцев можно взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит.
Задача 18
15-го января планируется взять кредит в банке на девять месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 25% больше суммы, взятой в кредит. Найдите r.
Задача 19
15-го января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условие его выплаты таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит?
Задача 20
15-го января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условие его выплаты таковы:
− 1-го числа k-ого месяца долг возрастёт на 1% по сравнению с концом предыдущего месяца;
− со 2-го по 14-е число k-того месяца необходимо выплатить часть долга;
− 15-го числа k-того месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит?
Задача 21
В июле планируется взять кредит в банке на сумму 9 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 3,6 млн рублей?
Задача 22
В июле планируется взять кредит в банке на сумму 9 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 1,5 млн рублей?
Задача 23
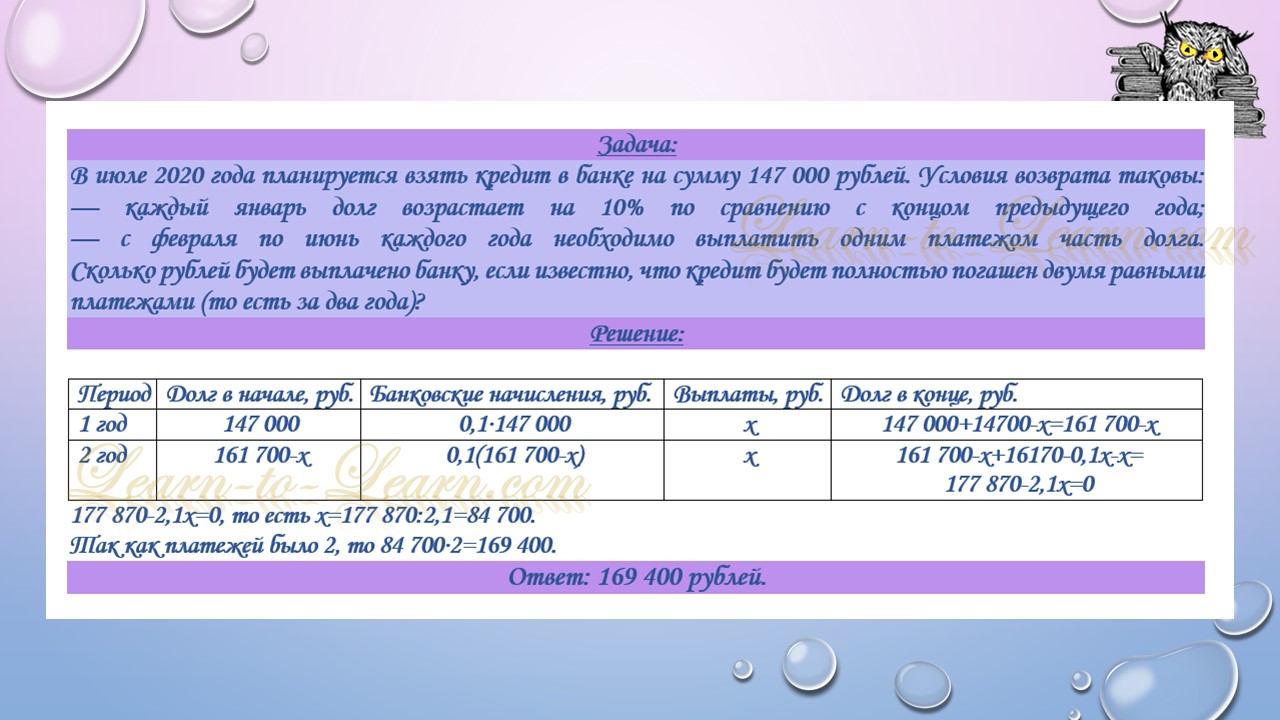
В июле 2020 года планируется взять кредит в банке на сумму 147 000 рублей. Условия его возврата таковы:
— каждый январь долг увеличивается на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей будет выплачено банку, если известно, что кредит будет полностью погашен двумя равными платежами, то есть за два года.
Задача 24
В июле планируется взять кредит в банке на сумму 5 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 7,5 млн рублей?
Задача 25
Вадим является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно часов в неделю, то за эту неделю они производят t единиц товара.
За каждый час работы на заводе, расположенном в первом городе, Вадим платит рабочему 500 рублей, а на заводе, расположенном во втором городе, — 300 рублей.
Вадим готов выделять 1 200 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Задача 26
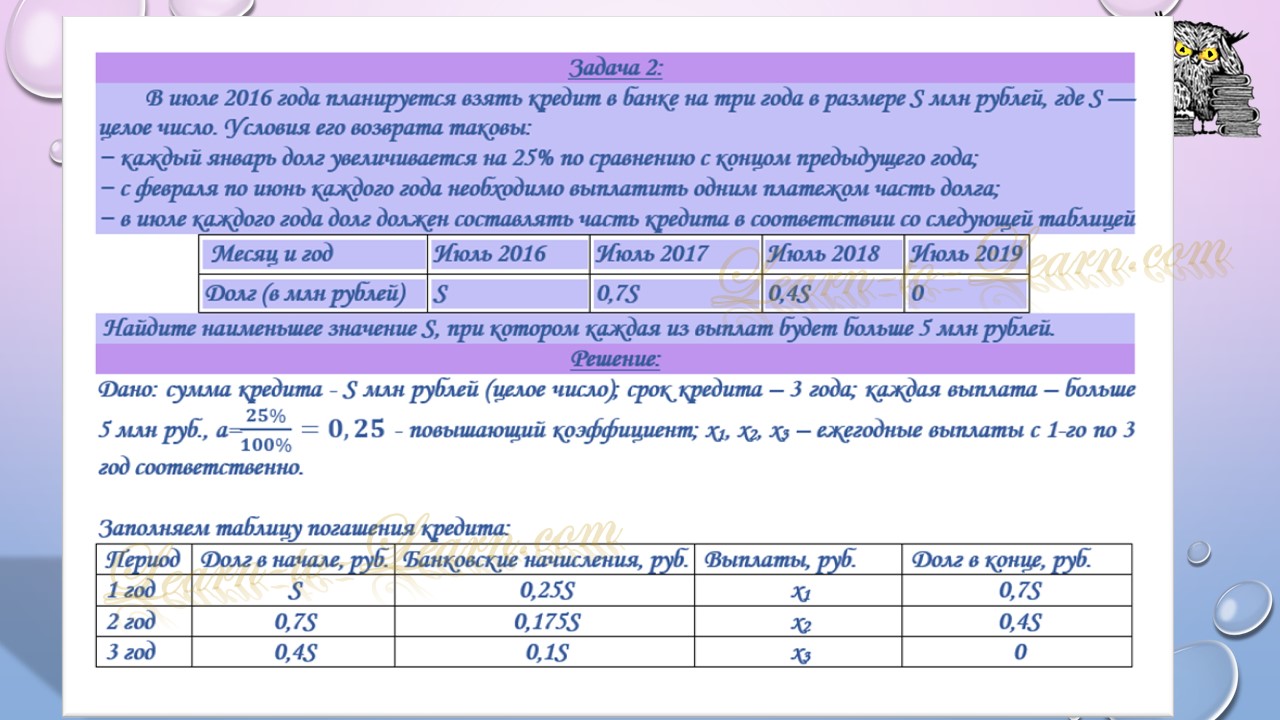
22. В июле 2016 года планируется взять кредит в банке на четыре года в размере S млн рублей, где S — натуральное число. Условия его возврата таковы:
— каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2016 | Июль 2017 | Июль 2018 | Июль 2019 | Июль 2020 |
| Долг (в млн рублей) | S | 0,7S | 0,5S | 0,3S | 0 |
Найдите наименьшее значение S, при котором общая сумма выплат будет составлять целое число миллионов рублей.
Задачи с фразой «долг должен быть на одну и ту же величину меньше долга на предыдущий период».
- В июле 2025 года планируется взять кредит в банке на сумму 900 тысяч рублей на 10 лет. Условия его возврата таковы:
- в январе 2026, 2027, 2028, 2029 и 2030 годов долг возрастает на 12% по сравнению с концом предыдущего года;
- в январе 2031, 2032, 2033, 2034 и 2035 годов долг возрастает на 8% по сравнению с концом предыдущего года;
- со февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
- к июлю 2035 года кредит должен быть погашен полностью.
- Найдите общую сумму выплат после полного погашения кредита.
- Ответ: 1440 тыс. руб.
- В июле 2025 года планируется взять кредит на 600 тыс. рублей. Условия его возврата таковы:
- в январе 2026, 2027 и 2028 годов долг возрастает на r% по сравнению с концом предыдущего года;
- в январе 2029, 2030 и 2031 годов долг возрастает на 15% по сравнению с концом предыдущего года;
- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
- к июлю 2031 года долг должен быть полностью погашен.
- Чему равно r, если общая сумма выплат составит 930 тысяч рублей?
- Ответ: 16.
- В августе со 2 по 15-е число 2026 года планируется взять кредит на 1200 тысяч рублей. Условия его возврата таковы:
- первого числа каждого месяца кредит увеличивается на 1%;
- со 2 по 15 числа каждого месяца, на протяжении следующих десять месяцев, долг должен уменьшаться на одну и ту же величину по сравнению с предыдущим месяцем;
- на одиннадцатый месяц перед начислением процентов остаток кредита будет составлять 400 тыс. руб., после чего он погашается одним платежом.
- Чему равна общая сумма выплат?
- Ответ: 1 млн 288 тыс. руб.
- 15 января 2025 года планируется взять кредит в банке на сумму 900 тысяч рублей на 31 месяц. Условия его возврата таковы:
- 1-го числа каждого месяца долг увеличивается на 2% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца с 1-го по 30-й (с февраля 2025 года по июль 2027 года включительно) долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца;
- 15 июля 2027 года долг составит 300 тысяч рублей;
- 15 августа 2027 года кредит должен быть погашен полностью.
- Найдите общую сумму выплат после полного погашения кредита.
- Ответ:1 млн 272 тыс. руб.
- В июле планируется взять кредит в банке на сумму 5 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
- каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
- На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 7,5 млн рублей?
- Ответ: 4 года.
- Был выдан кредит на 550000 рублей. Известно, что банк каждый год увеличивает сумму кредита на 20 процентов, после чего происходит платеж. Кредит был полностью выплачен за 2 года, причем платежи были равными. Найдите общую сумму, выплаченную клиентом банку.
- Ответ: 720 000 рублей.(Основная волна.2020г.)
- В июле планируется взять кредит в банке на сумму 6 млн рублей на срок 15 лет. Условия его возврата таковы:
- каждый январь долг возрастает на x% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
- Найдите x, если известно, что наибольший платёж по кредиту составит не более 1,9 млн рублей, а наименьший — не менее 0,5 млн рублей.
- Ответ: 25 (Основная волна. Дальний восток)
- В июле планируется взять кредит в банке на сумму 14 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
- каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
- Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платёж составит 3,85 млн рублей? (Считайте, что округления при вычислении платежей не производятся).
- Ответ: 17.5 млн. руб. (Основная волна.2019г)
Задачи с заданным изменением долга
- 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
- 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
-
Дата 15.01 15.02 15.03 15.04 15.05 15.06 15.07 Долг (в миллионах рублей) 1 0,6 0,4 0,3 0,2 0,1 0 - Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.
- Ответ : 7. (Демонстрационная версия ЕГЭ—2021.)
- В июле 2026 года планируется взять кредит в банке на пять лет в размере S тыс. рублей. Условия его возврата таковы:
- каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле 2027, 2028 и 2029 долг остаётся равным S тысяч рублей;
- выплаты в 2030 и 2031 годах равны по 360 тысяч рублей;
- к июлю 2031 долг будет выплачен полностью.
- Найдите общую сумму выплат за пять лет.
- Ответ: 1050 тыс. рублей. (Основная волна. Санкт-Петербург 2020 и 2017 г.).
- В кредит взяли 220 тыс. рублей на 5 лет под r% годовых. По условиям кредита, на конец первых трех лет задолженность остается неизменной и равной 220 тысячам рублей, а выплаты последних двух лет равны. На конец пятого года кредит должен быть погашен.
- Найдите r если известно, что сумма всех выплат составит 420 тысяч рублей.
- Ответ: 20. (Основная волна. Краснодар. 2020г.)
- 15-го декабря планируется взять кредит в банке на 13 месяцев. Условия возврата таковы:
- 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца с 1-го по 12-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
- к 15-му числу 13-го месяца кредит должен быть полностью погашен.
- Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 804 тысячи рублей?
- Ответ: 700 тыс. руб.(Основная волна.2018)
Задачи на исследование квадратичной функции(прибыль, налоги)
- Строительство нового завода стоит 75 млн рублей. Затраты на производство x тыс. ед. продукции на таком заводе равны
млн рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит
Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 3 года?
- Ответ: 9.(Демонстрационная версия ЕГЭ—2021.)
- Пенсионный фонд владеет ценными бумагами, которые стоят
тыс. рублей в конце года
В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться в
раз. Пенсионный фонд хочет продать ценные бумаги в конце такого года, чтобы в конце двадцать пятого года сумма на его счёте была наибольшей. Расчёты показали, что для этого ценные бумаги нужно продавать строго в конце двадцать первого года. При каких положительных значениях r это возможно?
- Ответ: (41/400;43/100)
Задачи про вклады
- Планируется открыть вклад на 4 года, положив на счет целое число млн рублей. В конце каждого года он увеличивается на 10%, а в начале третьего и четвертого года вклад пополняется на 5 млн рублей. Найдите наименьший первоначальный вклад, при котором начисленные проценты за весь срок будут более 10 млн рублей.
- Ответ:19. (Резервный день. 2020г.)
- Вадим является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно
часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе, Вадим платит рабочему 200 рублей, а на заводе, расположенном во втором городе, — 300 рублей. Вадим готов выделять 1 200 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
- Ответ: 100. (Резервный день. 2016)
- Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 3t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 4t единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей. Григорий готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
- Ответ:500. (Досрочная волна.2015)
Задача о доходах населения
Задача 1
В регионе A среднемесячный доход на душу населения в 2014 году составлял 43 740 рублей и ежегодно увеличивался на 25%. В регионе B среднемесячный доход на душу населения в 2014 году составлял 60 000 рублей. В течение трёх лет суммарный доход жителей региона B увеличивался на 17% ежегодно, а население увеличивалось на m% ежегодно. В 2017 году среднемесячный доход на душу населения в регионах A и B стал одинаковым. Найдите m.
-
- Ответ:4. (Досрочная волна-2018)
Задача 2
В июле 2019 года планируется взять кредит в банке на три года в размере S тысяч рублей, где S — целое число. Условия его возврата таковы:
− каждый январь долг увеличивается на 30% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
− в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей
| Месяц и год | Июль 2019 | Июль 2020 | Июль 2021 | Июль 2022 |
| Долг (в тыс. рублей) | S | 0,7S | 0,3S | 0 |
Найдите наибольшее значение S, при котором каждая из выплат будет больше 3 млн рублей.
Ответ: 8 млн рублей.
Задача 3
В июле 2026 года планируется взять кредит в банке на три года в размере S тысяч рублей, где S — целое число. Условия его возврата таковы:
− каждый январь долг увеличивается на 20% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
− в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей
| Месяц и год | Июль 2026 | Июль 2027 | Июль 2028 | Июль 2029 |
| Долг (в тыс. рублей) | S | 0,8S | 0,4S | 0 |
Найдите наибольшее значение S, при котором каждая из выплат будет меньше 5 млн рублей.
Ответ: 8 000 000 рублей.
Задача 4
В июле 2020 года планируется взять кредит в банке на четыре года в размере S тысяч рублей, где S — целое число. Условия его возврата таковы:
− каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
− в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей
| Месяц и год | Июль 2016 | Июль 2017 | Июль 2018 | Июль 2019 | Июль 2020 |
| Долг (в тыс. рублей) | S | 0,8S | 0,5S | 0,1S | 0 |
Найдите наибольшее значение S, при котором общая сумма выплат будет меньше 50 млн рублей.
Ответ: 36 000 000 рублей.
Задача 5
В июле 2020 года планируется взять кредит в банке на четыре года в размере S тысяч рублей, где S — целое число. Условия его возврата таковы:
− каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
− в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей
| Месяц и год | Июль 2020 | Июль 2021 | Июль 2022 | Июль 2023 | Июль 2024 |
| Долг (в тыс. рублей) | S | 0,8S | 0,6S | 0,4S | 0 |
Найдите наибольшее значение S, при котором общая сумма выплат будет меньше 50 млн рублей.
Ответ: 29 000 000 рублей.
Задача 6
Строительство нового завода стоит 220 млн рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны 0,5х2+х+7 млн рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит рх-(0,5х2+х+7). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При этом в первый год p = 9, а далее каждый год возрастает на 1 тыс. руб. за единицу. За сколько лет окупится строительство?
Ответ: 5 лет.
Задача 7
В июле планируется взять кредит в банке на сумму 3 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платёж составит 0,24 млн рублей? (Считайте, что округления при вычислении платежей не производятся).
Ответ: 7,8 млн руб.
Задача 8
В июле планируется взять кредит в банке на сумму 7 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 17,5 млн рублей?
Ответ: 14 лет.
Задача 9
В июле планируется взять кредит в банке на сумму 8 млн рублей на срок 4 года. Условия его возврата таковы:
— каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 4 млн рублей, а наименьший — не менее 2,5 млн рублей.
Ответ: 25%.
Задача 10
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— Каждый январь долг увеличивается на r% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 75 000 руб, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 123 000 руб, то кредит будет полностью погашен за 2 года. Найдите r.
Ответ:25%
Задача 11
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— Каждый январь долг увеличивается на r% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 77 760 руб, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 131 760 руб, то кредит будет полностью погашен за 2 года. Найдите r.
Ответ: 20%
Задача 12
В июле 2022 года планируется взять кредит на сумму 419 375 рублей. Условия возврата таковы:
— в январе каждого года долг увеличивается на 20% по сравнению с предыдущим годом;
— с февраля по июнь нужно выплатить часть долга одним платежом.
Сколько рублей будет выплачено банку, если известно, что кредит будет полностью погашен четырьмя равными платежами (то есть за четыре года)?
Ответ: 648 000 рублей.
Задача 13
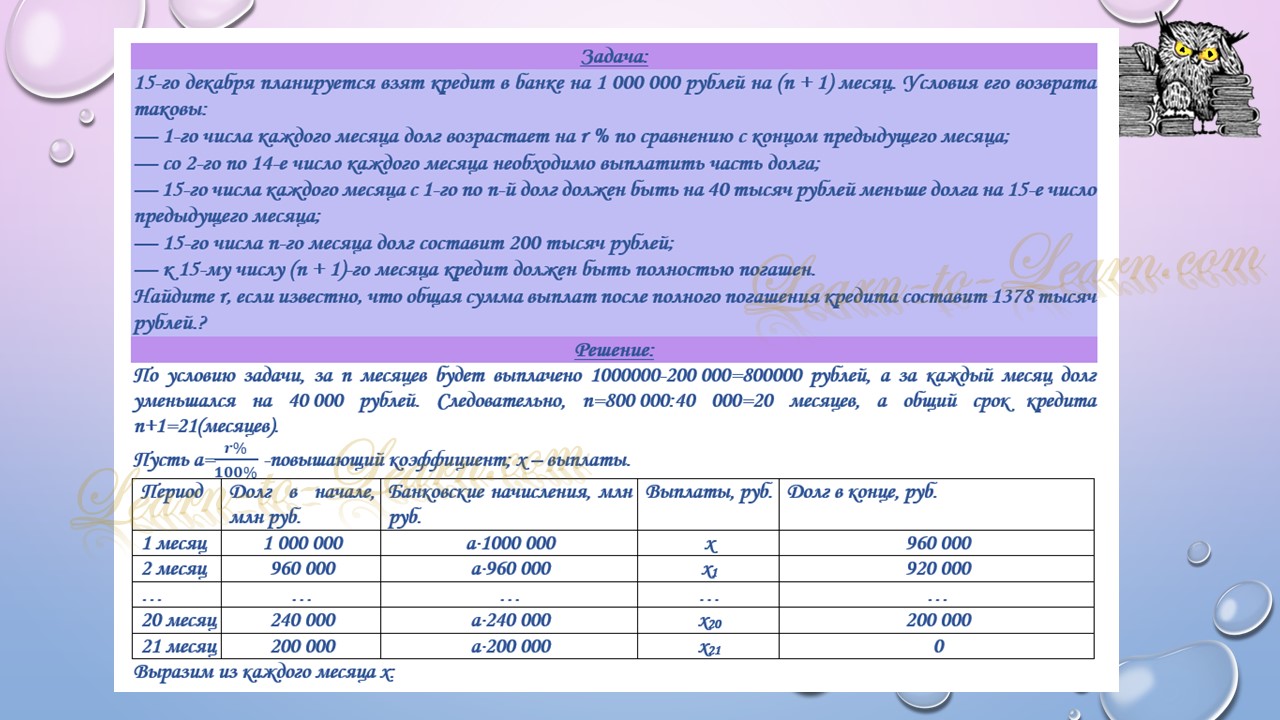
15-го декабря планируется взят кредит в банке на 1200 тысяч рублей на (n+1) месяц. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по n-й долг должен быть на 80 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— 15-го числа n-го месяца долг составит 400 тысяч рублей;
— к 15-му числу (n+1)-го месяца кредит должен быть полностью погашен.
Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1288 тысяч рублей.
Ответ: 1%.
Задача 14
15-го декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 21-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1604 тысяч рублей?
Ответ: 1 100 000 рублей.
Задача 15
15-го декабря планируется взять кредит в банке на сумму 300 тысяч рублей на 21 месяц. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 20-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— 15-го числа 20-го месяца долг составит 100 тысяч рублей;
— к 15-му числу 21-го месяца кредит должен быть полностью погашен.
Найдите общую сумму выплат после полного погашения кредита.
Ответ: 384 000 рублей.
Задача 16
15-го декабря планируется взят кредит в банке на 600 000 рублей на 26 месяцев. Условия его возврата таковы:
− 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
− cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
− 15-го числа с 1 по 25 месяц долг должен уменьшаться на одну и ту же сумму;
− 15-го числа 26 месяца долг должен быть погашен.
Сколько тысяч рублей составляет долг на 15 число 25 месяца, если всего было выплачено 691 тысяч рублей?
Ответ: 100 000 рублей.
Задача 17
15-го декабря планируется взять кредит в банке на 11 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 10-й долг должен быть на 80 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 11-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 10-го месяца, если общая сумма выплат после полного погашения кредита составит 1198 тысяч рублей?
Ответ: 200 000 рублей.
Задача 18
15-го декабря планируется взять кредит в банке на 26 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 25-й долг должен быть на 20 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 26-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 25-го месяца, если общая сумма выплат после полного погашения кредита составит 1407 тысяч рублей?
Ответ: 400 000 рублей.
Задача 19
15-го декабря планируется взять кредит в банке на сумму 1100 тысяч рублей на 31 месяц. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 30-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 31-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 30-го месяца, если общая сумма выплат после полного погашения кредита составит 1503 тысячи рублей?
Ответ: 200 000 рублей.
Задача 20
15-го декабря планируется взять кредит в банке на сумму 1 000 000 рублей на 11 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 10-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 11-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 10-го месяца, если общая сумма выплат после полного погашения кредита составит 1231 тысячи рублей?
Ответ: 400 000 рублей.
Задача 21
Зависимость количества Q (в шт., 0≤Q≤20000 купленного у фирмы товара от цены P (в руб. за шт.) выражается формулой Q=20 000-P. Затраты на производство Q единиц товара составляют 6000Q+4 000 000 рублей. Кроме затрат на производство, фирма должна платить налог t рублей (0<t<10000) с каждой произведённой единицы товара. Таким образом, прибыль фирмы составляет PQ-6000Q-4000000-tQ рублей, а общая сумма налогов, собранных государством, равна tQ рублей.
Фирма производит такое количество товара, при котором её прибыль максимальна. При каком значении t общая сумма налогов, собранных государством, будет максимальной?
Ответ: 7 000 рублей.
Задача 22
Зависимость объёма Q (в шт.) купленного у фирмы товара от цены Р (в руб. за шт.) выражается формулой Q=15 000-P, 1000≤P≤15000. Доход от продажи товара составляет РQ рублей. Затраты на производство Q единиц товара составляют 3000Q+5 000 000 рублей. Прибыль равна разности дохода от продажи товара и затрат на его производство. Стремясь привлечь внимание покупателей, фирма уменьшила цену товара на 20%, однако её прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?
Ответ: 12,5%.
Задача 23
15-го декабря планируется взят кредит в банке на 700 тысяч рублей на (n+1) месяц. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
— cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по n-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— 15-го числа n-го месяца долг составит 300 тысяч рублей;
— к 15-му числу (n+1)-го месяца кредит должен быть полностью погашен.
Найдите n, если известно, что общая сумма выплат после полного погашения кредита составит 755 тысяч рублей.
Ответ: 10 месяцев.