ЕГЭ-математика-профиль-задание 3

 Если Вы сами не смогли решить задачу, то ВЫУЧИТЕ представленное решение, а не просто просмотрите или спишите его.

1. В треугольнике АВС угол С равен 46º, AD и BE — биссектрисы, пересекающиеся в точке О. Найдите угол АОВ. Ответ дайте в градусах.

1 шаг. Наношу на чертеж все известное, обозначу вопрос задачи как х.

2 шаг. Вижу на чертеже треугольники. Перечисляю все, что о них знаю, нахожу все, что могу.

1.В треугольнике АВС больше всего известных: 

• • угол С = 46º;
  • AD и BE — биссектрисы, они делят ∠А и ∠В пополам, обозначу каждую половину ∠А — z; ∠B — y; то есть ∠А=2z, ∠B=2y;
  • могу найти сумму ∠А и ∠В по теореме о сумме углов в треугольнике: ∠A+∠B+∠C=180º, подставляю все известное: 2z+2y+46º=180º, то есть z+у=67º;
  • в этом треугольнике больше не могу ничего найти;
  • наношу дополнительную информацию на чертеж.
  • 

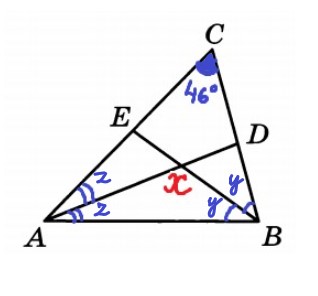
2. В треугольнике АОВ находится угол, который нужно найти:

• • сумма углов z и y равна 67º;
  • по теореме о сумме углов в треугольнике могу найти угол АОВ: ∠АОВ+∠ОАВ+∠ОВА=180º, подставляю все известное: ∠АОВ+67º=180º, то есть ∠АОВ=113º.

Ответ: 113.

2. В треугольнике АВС высота СН равна 6, АВ=ВС, АС=8. Найдите синус угла АСВ.

1 шаг. Наношу на чертеж все известное, вопрос задачи обозначить на чертеже не могу (тригонометрические функции на чертеже не обозначаются).

2 шаг. Какие фигуры вижу, что о них знаю или могу узнать?

Вижу на чертеже треугольники. Перечисляю все, что о них знаю, нахожу все, что могу.

1.В треугольнике АВН больше всего известных: 

• • угол Н = 90º, то есть треугольник прямоугольный;
  • катет НС=6; гипотенуза АС=8;  (будет не нужен);
  • могу найти синус ∠А: sin ∠A = 6/8=0,75;
  • могу найти косинус и синус угла НСВ, катет АН, площадь треугольника и многое другое (все это будет не нужно, поэтому решение размещать не буду);
  • в этом треугольнике больше не могу ничего найти;
  • разместить дополнительную информацию на чертеже не могу (тригонометрические функции на чертеже не подписываются).

2. В треугольнике АВС знаю, что:

• • ∠А=∠АСВ, так как треугольник равнобедренный;
  • так как углы равны, то равны их синусы, а синус ∠А уже найден.

Ответ: 0,75.

3. В четырехугольнике АВСD вписана окружность, АВ=13, CD=18. Найдите периметр четырехугольника.

1 шаг. Нанесем на чертеж все известное, вопрос задачи на чертеже обозначить не могу (периметр на чертеже не обозначается).

2 шаг. Какие фигуры вижу, что о них знаю или могу узнать?

Вижу на чертеже четырехугольник и окружность. Перечисляю все, что о них знаю, нахожу все, что могу.

1.В четырехугольнике больше всего известных: 

• • • в четырехугольник вписана окружность, значит, суммы противолежащих сторон этого четырехугольника равны: АВ+CD=ВС+DA, то есть ВС+DA=18+13=31;
    • периметр четырехугольника — это сумма всех его сторон:  АВ+ВС+CD+DA=P, то есть 31+31=62.

Ответ: 62.

4. Через концы А и В дуги окружности с центром О проведены касательные СА и СВ. Угол САВ равен 39º. Найдите угол АОВ. Ответ дайте в градусах.

1 шаг. Нанесем на чертеж все известное и обозначим главный вопрос задачи.

2 шаг. Какие фигуры вижу, что о них знаю или могу узнать?

Вижу на чертеже треугольники и четырехугольники. Перечисляю все, что о них знаю, нахожу все, что могу.

1.В треугольнике ВСА больше всего известных: 

• • • известен ∠САВ = 39º;
    • треугольник ВСА равнобедренный (так как касательные ВС и СА проведены из одной точки);
    • ∠САВ=∠СВА=39º (углы при основании равнобедренного треугольника равны);
    • ∠С=180º-39º-39º=102º (по теореме о сумме углов в треугольнике);

2. В четырехугольнике АСВО также много известных величин:

• • • известен ∠С=102º;
    • ∠В=∠А=90º (углы, которые образованы касательными и радиусом);
    • ∠АОВ=360º-2•90º-102º=78º (сумма углов четырехугольника равна 360º).

Ответ: 78.

5. Четырехугольник АВСD вписан в окружность. Угол АВС равен 106º, угол CAD равен 69º. Найдите угол ABD. Ответ дайте в градусах.

1 шаг. Нанесем на чертеж все известное и обозначим главный вопрос задачи.

• • • в задаче идет речь только о вписанных углах, подпишем их значения между точками, на которые они опираются (это не имеет отношения величине дуги окружности между этими точками)

2 шаг. Какие фигуры вижу, что о них знаю или могу узнать?

Вижу, что АС=АD+DC, то есть AD=AC-DC=106º-69º=37º.

Ответ: 37.

6. Четырехугольник АВСD вписан в окружность. Угол ВAD равен 127º. Найдите угол BCD. Ответ дайте в градусах.

1 шаг. Нанесем на чертеж все известное и обозначим главный вопрос задачи.

2 шаг. Какие фигуры вижу, что о них знаю или могу узнать?

Вижу на чертеже четырехугольник. Перечисляю все, что о нем знаю, нахожу все, что могу.

• • • ∠А=127º;
    • ∠С+∠А=180º (четырехугольник можно вписать в окружность, если сумма противолежащих улов равна 180º), то есть ∠С=180º-127º=53º.

Ответ: 53.

7. Градусная мера дуги АВ окружности, не содержащей точку D, равна 106º. Градусная мера дуги DE окружности, не содержащей точку А, равна 48º. Найдите угол АСB. Ответ дайте в градусах.

1 шаг. Нанесем на чертеж все известное и обозначим главный вопрос задачи.

2 шаг. Какие фигуры вижу, что о них знаю или могу узнать?

Вижу на чертеже треугольник DAC. Перечисляю все, что о нем знаю, нахожу все, что могу.

• • • • ∠А=24º (вписанный угол равен половине дуги, на которую опирается);
      • внешний угол ΔDAC ∠BDA= 53º (вписанный угол равен половине дуги, на которую опирается);
      • ∠BDA=∠А+∠С (внешний угол треугольника), то есть ∠C=53º-24º=29º.

Ответ: 29.

8. Радиус окружности описанной около треугольника АВС равен 2√3. Найдите АВ, если угол АСВ равен 120º.

Чтобы найти сторону треугольник, если известен радиус окружности и угол напротив, то воспользуемся готовой формулой, дополнительных шагов не требуется: 

   

   

Ответ: 6.

9. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 15 и 17.

1 шаг. Для выполнения этой задачи чертеж не требуется, желающие могут его начертить самостоятельно.

2 шаг. Какие фигуры вижу, что о них знаю или могу узнать?

1.    

   • где а и в катеты треугольника;
2. найдем недостающий катет по теореме Пифагора:

      

3. S=15•8:2=60/

Ответ: 60.

10. В треугольнике АВС средняя линия DE параллельна стороне АВ. Найдите площадь треугольника АВС, если площадь трапеции АВЕD равна 48.

1 шаг. Чертеж уже дан, подписывать дополнительно ничего не надо.

2 шаг. Какие фигуры вижу, что о них знаю или могу узнать?

1.Вижу на чертеже треугольник DCЕ. Перечисляю все, что о нем знаю, нахожу все, что могу.

• • • • ΔDCE∼ΔАСВ (по двум равным углам — соответственные углы при параллельных прямых), коэффициент подобия k= 2 (так как проведена средняя линия);
      • площадь ΔDCE в 4 раза меньше площади ΔАСВ (площади подобных фигур отличаются в k² раз);

2.Трапеция ADEB:

• • • • если ΔDCE занимает 1 из 4 частей площади ΔАСВ, то трапеция занимает 3 части из 4;
      • 
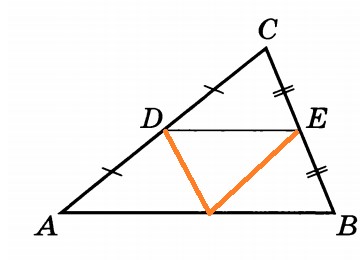
      • если площадь 3х частей 48, то площадь одной части 48:3=16;
      • весь треугольник — 4 части, то есть площадь всего треугольника 16•4=64.

Ответ: 64.

11. Площадь параллелограмма равна 145. Найдите площадь параллелограмма, вершины которого являются серединами сторон заданного параллелограмма.

1 шаг. Выполним чертеж:

• разобьем внутренний параллелограмм на одинаковые треугольники, видим, что внутренний параллелограмм состоит из 4 одинаковых треугольников, а внешний из 8 таких же равных треугольников, значит, площади этих параллелограммов отличаются в 2 раза:

S=145:2=72,5

Ответ: 72,5.

12. Один из углов прямоугольного треугольника равен 66º. Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.

1 шаг. Нанесем на чертеж все известное и обозначим главный вопрос задачи. (почему именно угол В=66º? попробуйте решить эту задачу, если угол А равен 66º, и поймете)

2 шаг. Какие фигуры вижу, что о них знаю или могу узнать?

1.В треугольнике ВСН много известных:

• • • • ∠В=66º, ∠ВНС=90º (по условию);
      • ∠ВСН=90º-66º=24º (сумма острых углов прямоугольного треугольника равна 90º);

2.В треугольнике АВС много известных:

• • • • ∠С=90º (по условию);
      • ∠ВСD=45º (так как CD биссектриса прямого угла), кроме того по чертежу видно, что ∠ВСD=∠НСD+∠ВСН, то есть ∠ВСН=45º-24º=21º.

Ответ: 21.

13. Острые углы прямоугольного треугольника равны 80º и 10º. Найдите угол между медианой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.

1шаг Нанесем на чертеж все известное:

2 шаг Какие фигуры вижу, что о них знаю или могу узнать?

В Δ АМС много известных:

• ∠ А=10º (по условию);
• АМ=МС, так как МС — медиана, проведенная из прямого угла треугольника АВС; то есть ΔАСМ — равнобедренный, то есть ∠АСМ= ∠ А=10º ;

В ΔАВС много известных:

• ∠С=90º (по условию);
• ∠АСD=45º (так как CD — биссектриса);
• ∠АСМ= 10º (уже найдено);
• ∠МСD= 45º-10º= 35º.

3. Ответ: 35.

14. Основания трапеции равны 15 и 26. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

1 шаг Нанесем на чертеж все известное.

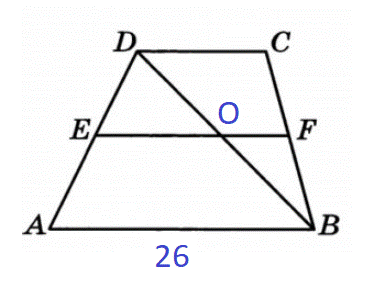
2 шаг Какие фигуры вижу, что о них знаю или могу узнать?

• в ΔADE есть известные величины:
  • • АВ=26 (по условию);
    • ЕО-средняя линия треугольника (проходит через середины боковых сторон по условию);
    • ЕО=АВ/2=26/2=13 (по свойству средней линии).

3 шаг Ответ: 13.

15. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 41, отсекает треугольник, периметр которого равен 83. Найдите периметр трапеции.

1 шаг Нанесем на чертеж все известное.

2 шаг Какие фигуры вижу, что о них знаю или могу узнать?

• в параллелограмме DCBE есть известные величины:
  • • DC=EB=41 (по условию и свойству параллелограмма);
    • DE=CB (по свойству параллелограмма).
• в ΔADE есть известные величины:
  • • DE=СВ
    • P=83 (по условию); то есть я знаю сумму сторон AD, DE, AE или AD,CB, AE (этот набор сторон для нахождения периметра трапеции важнее, так как включает в себя только части трапеции).
• в трапеции ABCD:
  • • AE+AD+CB=83; DC+EB=82;
    • PABCD=83+82=165.

3 шаг Ответ: 165.

16. В треугольнике со сторонами 8 и 4 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 1. Чему равна высота, проведенная ко второй стороне?

1 шаг. Построение в данной задаче не требуется.

2 шаг. Какие фигуры даны, что о них знаю или могу узнать?

• в треугольнике даны высота и сторона, такие термины встречаются в формуле нахождения площади треугольника; найду площадь: S=8•1:2=4;
• теперь знаю площадь треугольника и другую сторону, с помощью той же самой формулы найду высоту: (1) 4=4•h:2, то есть h=2.

3 шаг. Ответ: 2.

17. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 9. Найдите среднюю линию этой трапеции.

1 шаг. Выполняем чертеж, обозначаем на нем известное:

2 шаг. Какие фигуры даны, что о них знаю или могу узнать?

• Вижу два треугольника ADH и BCE, они равны (так как трапеция по условию равнобедренная), то есть АН=ЕВ=9; следовательно НЕ=10-9=1;
• Вижу прямоугольник НDСЕ, в нем DC=HE (по свойству прямоугольника), то есть DC=1;
• Вижу трапецию ABCD: основание АВ=10+9=19;
• Средняя линия трапеции равна полусумме оснований: (1+19)/2=10;

3 шаг. Ответ: 10.

18. Два угла треугольника равны 68º и 35º. Найдите тупой угол, который образуют высоты треугольника, выходящие из этих углов.

1 шаг. Нанесем на чертеж все известное и обозначим главный вопрос задачи:

2 шаг. Какие фигуры даны, что о них знаю или могу узнать?

Вижу ΔАВС, в нем многое известно:

• ∠А=68º и ∠С=35º (по условию);
• найдем угол В из треугольника АВС по теореме о сумме углов в треугольнике:

68º+35º+∠В=180º

∠В=77º

Вижу четырехугольник ОНВЕ, в нем многое известно:

• ∠ВНО=90º и ∠ВЕО=90º (так как СН и АЕ высоты);
• сумма углов в четырехугольнике 360º;
• х=360º=90º+90º+77º+х, то есть х=103º.

3 шаг. Ответ: 103.

19. Найдите угол АСО, если его сторона АС касается окружности, отрезок ОС пересекает окружность в точке В, а дуга АВ, заключенная внутри этого угла, равна 17º. Ответ дайте в градусах.

1 шаг. Чертеж уже выполнен.

2 шаг. Какие фигуры даны, что о них знаю или могу узнать?

Вижу ΔАОС, в нем многое известно:

• ∠ ОАС=90º, так как этот угол образован радиусом и касательной;
• ∠ АОС=17º, так как опирается на дугу АС;
• по теореме о сумме углов в треугольнике: 90º+17º+∠АСО=180º, то есть ∠АСО=73º.

Ответ: 73.

20. В треугольнике АВС известно, что АС=ВС, АВ=20, sinA=√5/3. Найдите длину стороны АС.

1 шаг. Нанесем на чертеж все известное и обозначим главный вопрос задачи (дополню чертеж высотой, так как синус угла А удобно рассматривать в прямоугольном треугольнике):

2 шаг. Какие фигуры даны, что о них знаю или могу узнать?

Вижу ΔАНС, в нем многое известно:

• ∠АНС=90º (СН — высота);
• АН=20:2=10 (СН — высота и медиана, по свойству равнобедренного треугольника);
• sin²A+cos²A=1, то есть  cosA=2/3;

• cosA=AH/AC, то есть АС=15.

3 шаг. Ответ: 15.

21. Основания равнобедренной трапеции равны 24 и 10. Радиус описанной окружности равен 13. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.

1 шаг. Нанесем на чертеж все известное и обозначим главный вопрос задачи:

• выполню дополнительные построения:
  • проведу радиусы (провожу радиусы так, чтобы получились полезные фигуры); (бессмысленный поступок: «проведу горизонтальные радиусы, потому что это удобно»);
  • проведу высоту трапеции (так, чтобы получились полезные фигуры);( бессмысленный поступок: «проведу высоту из вершин трапеции, потому что так мы делаем всегда»):

2 шаг. Какие фигуры даны, что о них знаю или могу узнать?

Вижу ΔАОВ, в нем многое известно:

• ОА=ОВ — радиусы окружности, то есть треугольник равнобедренный;
• ОН-высота и медиана, по свойству равнобедренного треугольника, то есть АН=НВ=10/2=5;

Вижу ΔАНО, в нем многое известно:

• треугольник прямоугольный;
• по теореме Пифагора, нахожу НО.

Вижу ΔDОC и ΔDОМ, в них выполняю те же самые шаги и нахожу ОМ.

3 шаг. HM=12+5=17.

4 шаг. Ответ: 17.

22. Найдите центральный угол, если он на 28º больше вписанного угла, опирающегося на ту же дугу. Ответ дайте в градусах.

1 шаг. Чертеж уже выполнен.

2 шаг. Какие фигуры даны, что о них знаю или могу узнать?

Вижу два угла:

• вписанный и центральный, которые опираются на одну дугу;
• центральный угол в два раза больше вписанного угол (по свойству) и центральный угол на 28 градусов больше вписанного угла (по условию); 
• обозначу вписанный угол как х, тогда центральный угол 2х, а их разница 2х-х=28, то есть х=28;
• центральный угол: 28º•2=56º.

Ответ: 56.

23. Около окружности описана трапеция, периметр которой равен 28. Найдите длину ее средней линии. 

1 шаг. Чертеж уже выполнен.

2 шаг. Какие фигуры даны, что о них знаю или могу узнать?

Вижу два угла:

• окружность вписана в четырехугольник, значит, суммы противолежащих сторон равны, то есть сумма каждой пары сторон равна 28/2=14;

Вижу трапецию:

• средняя линия равна полусумме оснсований, а полусумму мы уже нашли: 14:2=7.

Ответ: 7.

24. В треугольнике АВС угол С равен 90º, АВ=82, tgA=4/5. Найдите высоту СН.

1 шаг. Нанесем на чертеж все известное и обозначим главный вопрос задачи:

2 шаг. Какие фигуры даны, что о них знаю или могу узнать?

Вижу ΔАВС:

• тангенс угла А=4/5, то есть СВ/АС=4/5 (по определению тангенса), то есть могу записать, что СВ=4х, АС=5х;
• по теореме Пифагора: АС²+СВ²=АВ², то есть 16х²+25х²=82², отсюда х=2√41, тогда АС=10√41 и СВ=8√41;
• S=АС*СВ/2=10√41 *8√41/2=40•41, с другой стороны S=СН*АВ/2, то есть СН=40•41•2/82=40.

3 шаг. Ответ: 40.